Dịch bệnh Viêm đường hô hấp cấp Covid-19. Tính đến 9h30 ngày 6/3/2020 (giờ Việt Nam):
87 quốc gia và vùng lãnh thổ có người mắc bệnh.

Tính đến 9h30 ngày 6/3/2020 (giờ Việt Nam), quốc gia nào ngoài Trung Quốc có số ca nhiễm CoVid-19 cao nhất?
-
Hàn Quốc
-
Italy
-
Iran
-
Mỹ
-
Hàn Quốc
-
Italy
-
Iran
-
Mỹ
Một vật rơi tự do theo phương trình ${ }^{s=\frac{1}{2} g t^2(m)}$, với ${ }^g=9,8\left(\mathrm{~m} / \mathrm{s}^2\right)$ Vận tốc tức thời tại thời điểm $t=5(s)$ là:
-
$49(\mathrm{~m} / \mathrm{s})$
-
$122,5(\mathrm{~m} / \mathrm{s})$
-
$29,5(\mathrm{~m} / \mathrm{s})$
-
$10(\mathrm{~m} / \mathrm{s})$
Vận tốc tức thời tại thờ điêm ${ }^{t=t_0}$ là: $v\left(t_0\right)=s^{\prime}\left(t_0\right)$,
Giải chi tiết:
Ta có: $s^{\prime}=$ gt
Vận tốc tức thời tại thời điểm ${ }^{t=5(s)}$ là:
$$
v(5)=s^{\prime}(5)=5 g=49(\mathrm{~m} / \mathrm{s}) \text {. }
$$
-
$49(\mathrm{~m} / \mathrm{s})$
-
$122,5(\mathrm{~m} / \mathrm{s})$
-
$29,5(\mathrm{~m} / \mathrm{s})$
-
$10(\mathrm{~m} / \mathrm{s})$
Vận tốc tức thời tại thờ điêm ${ }^{t=t_0}$ là: $v\left(t_0\right)=s^{\prime}\left(t_0\right)$,
Giải chi tiết:
Ta có: $s^{\prime}=$ gt
Vận tốc tức thời tại thời điểm ${ }^{t=5(s)}$ là:
$$
v(5)=s^{\prime}(5)=5 g=49(\mathrm{~m} / \mathrm{s}) \text {. }
$$
Nghiệm của phương trình $\log _2(1-x)=2$ là:
-
$x=-3$
-
$x=-4$
-
$x=3$
-
$x=5$
-
$x=-3$
-
$x=-4$
-
$x=3$
-
$x=5$
Giải hệ phương trình $\left\{\begin{array}{l}2 x^2-5 x y+2 y^2=0 \\ 2 x^2-y^2=7\end{array}\right.$ .
-
$(1 ; 2),(-1 ;-2)$
-
$(-2 ; 1),(1 ; 2)$
-
$(1 ; 2),(1 ;-2)$
-
$(-1 ; 2),(1 ;-2)$
-
$(1 ; 2),(-1 ;-2)$
-
$(-2 ; 1),(1 ; 2)$
-
$(1 ; 2),(1 ;-2)$
-
$(-1 ; 2),(1 ;-2)$
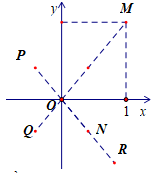
Trong mặt phẳng thực, cho số phức $z$ có điểm biểu diễn là $N$ . Biết rằng số phức ${ }^{w=\frac{1}{z}}$ được biểu diễn bởi một trong bốn điểm $M, P, Q, R$ như hình vẽ bên. Hỏi điểm biểu diễn của $w$ là điểm nào?
-
$M$
-
$P$
-
$Q$
-
$R$
-
$M$
-
$P$
-
$Q$
-
$R$
Trong không gian $O x y z$, cho hai điểm $A(1 ; 2 ; 3), B(2 ; 0 ; 5)$ . Viết phương trình mặt phẳng $(P)$ đi qua điểm $A$ và vuông góc với đường thẳng $A B$ .
-
$x-2 y+2 z-3=0$
-
$x+2 y+2 z+11=0$
-
$x-2 y+2 z-14=0$
-
$x+2 y+2 z-11=0$
-
$x-2 y+2 z-3=0$
-
$x+2 y+2 z+11=0$
-
$x-2 y+2 z-14=0$
-
$x+2 y+2 z-11=0$
Trong không gian với hệ tọa độ $O x y z$, cho hai điểm $A(1 ; 0 ; 1)$ và $B(4 ; 2 ;-2)$ . Độ dài đoạn thẳng $A B$ bằng:
-
$\sqrt{22}$
-
2
-
4
-
22
-
$\sqrt{22}$
-
2
-
4
-
22
Số giả trị nguyên của $x$ thỏa mãn bất phương trình $\frac{x^2}{\sqrt{x-1}}<\frac{2 x+8}{\sqrt{x-1}}$ là
-
2
-
4
-
5
-
6
-
2
-
4
-
5
-
6
Giải phương trình $\cos 2 x+5 \sin x-4-0$ .
-
$x=\frac{\pi}{2}+k 2 \pi$
-
$x=\frac{\pi}{3}+k \pi$
-
$x=-\frac{\pi}{2}+k \pi$
-
$x=k 2 \pi$
-
$x=\frac{\pi}{2}+k 2 \pi$
-
$x=\frac{\pi}{3}+k \pi$
-
$x=-\frac{\pi}{2}+k \pi$
-
$x=k 2 \pi$
Litva sẽ tham gia vào cộng đồng chung châu Âu sử dụng đồng Euro là đồng tiền chung vào ngày 01 tháng 01 năm 2015. Để kỷ niệm thời khắc lịch sữ chung này, chính quyền đất nước này quyết định dủng 122550 đồng tiền xu Litas Lithuania cũ của đất nước để xếp một mô hình kim tự tháp (như hình vẽ bên). Biết rằng tầng dưới cùng có 4901 đồng và cứ lên thêm một tầng thì số đồng xu giảm đi 100 đồng. Höi mô hình Kim tự tháp này có tất cả bao nhiêu tầng?

-
50
-
54
-
49
-
55
-
50
-
54
-
49
-
55
Họ nguyên hàm $\int \frac{x^3+x^2-5}{x^2+x-2} d x$ là:
-
$\frac{x^2}{2}-\ln |x-1|+3 \ln |x+2|+C$
-
$\frac{x^2}{2}+3 \ln |x-1|-\ln |x+2|+C$
-
$\frac{x^2}{2}+\ln |x-1|-\ln |x+2|+C$
-
$x-\ln |x-1|+3 \ln |x+2|+C$
-
$\frac{x^2}{2}-\ln |x-1|+3 \ln |x+2|+C$
-
$\frac{x^2}{2}+3 \ln |x-1|-\ln |x+2|+C$
-
$\frac{x^2}{2}+\ln |x-1|-\ln |x+2|+C$
-
$x-\ln |x-1|+3 \ln |x+2|+C$
Cho hàm số $f(x)$ có đồ thị như hình vẽ bên. Bất phương trình $f\left(e^x\right)
-
${ }^{m>-\frac{2}{1011}}$
-
$m>-\frac{4}{1011}$
-
$m \geq-\frac{4}{3 e+2019}$
-
$m>\frac{f(e)}{3 e+2019}$
Đặt $e^x=t(t>0)$ . Ta đưa bất phương trình đã cho thánh bất phương trình ần $t$, từ đó lập luận để có phương trình ẩn $t$ có nghiệm thuộc (1;e).
Ta chú ý rằng hàm số $y=f(x)$ và $y=f(t)$ có tính chất giống nhau
Nên từ đồ thị hàm số đã cho ta
Suy ra tính chất hàm $f(t)$ .
Sử dụng phương pháp hàm số để tim $m$ sao cho bất phương trình có nghiệm.
Bất phương trình $m>f(X)$ có nghiệm trên $(a ; b)$ khi $m>\min _{[a ; i \mid} f(X)$ .
Giải chi tiết:
Xét bất phương trình $f\left(e^x\right)<m\left(3 e^x+2019\right)$
Đặt $e^x=t(t>0)$ với: $x \in(0 ; 1) \Rightarrow t \in\left(e^0 ; e^1\right) \Rightarrow t \in(1 ; e)$.
Để bất phương trinh $\left(^*\right)$ có nghiệm $x \in(0 ; 1)$ thì bất phương trình (1) có nghiệm $t \in(1 ; e)$,
Ta xét hàm $g(t)=\frac{f(t)}{3 t+2019}$ trên $(1 ; e)$.
Ta có
$$
g^{\prime}(t)=\frac{f^{\prime}(t)(3 t+2019)-3 f(t)}{(3 t+2019)^2} .
$$
Nhận xét rằng đồ thị hàm số $y=f(t)$ có tính chất giống với đồ thị hàm số $y=f(x)$ nên ? khoàng $(1 ; e)$ ta thấy rằng $f(t)<0$ và đồ thị hàm số đi lên từ trái qua phải hay hàm số đồng b: $(1 ; e)_{\text {nền }} f^{\prime}(t)>0$.
Từ đó
$$
g^{\prime}(t)-\frac{f^{\prime}(t)(3 t+2019)-3 f(t)}{(3 t+2019)^2}>0
$$
với $t \in(1 ; e)$ hay hàm số $g(t)$ đồng biến trên $(1 ; e)$
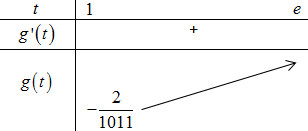
Từ BBT ta thây để bất phương trình $m>\frac{f(t)}{3 t+2019}$ với $t \in(1 ; e)$ thì $m>\min _{[1: \mathrm{i}} g(t) \Leftrightarrow m>-\frac{2}{1011}$.
-
${ }^{m>-\frac{2}{1011}}$
-
$m>-\frac{4}{1011}$
-
$m \geq-\frac{4}{3 e+2019}$
-
$m>\frac{f(e)}{3 e+2019}$
Đặt $e^x=t(t>0)$ . Ta đưa bất phương trình đã cho thánh bất phương trình ần $t$, từ đó lập luận để có phương trình ẩn $t$ có nghiệm thuộc (1;e).
Ta chú ý rằng hàm số $y=f(x)$ và $y=f(t)$ có tính chất giống nhau
Nên từ đồ thị hàm số đã cho ta
Suy ra tính chất hàm $f(t)$ .
Sử dụng phương pháp hàm số để tim $m$ sao cho bất phương trình có nghiệm.
Bất phương trình $m>f(X)$ có nghiệm trên $(a ; b)$ khi $m>\min _{[a ; i \mid} f(X)$ .
Giải chi tiết:
Xét bất phương trình $f\left(e^x\right)<m\left(3 e^x+2019\right)$
Đặt $e^x=t(t>0)$ với: $x \in(0 ; 1) \Rightarrow t \in\left(e^0 ; e^1\right) \Rightarrow t \in(1 ; e)$.
Để bất phương trinh $\left(^*\right)$ có nghiệm $x \in(0 ; 1)$ thì bất phương trình (1) có nghiệm $t \in(1 ; e)$,
Ta xét hàm $g(t)=\frac{f(t)}{3 t+2019}$ trên $(1 ; e)$.
Ta có
$$
g^{\prime}(t)=\frac{f^{\prime}(t)(3 t+2019)-3 f(t)}{(3 t+2019)^2} .
$$
Nhận xét rằng đồ thị hàm số $y=f(t)$ có tính chất giống với đồ thị hàm số $y=f(x)$ nên ? khoàng $(1 ; e)$ ta thấy rằng $f(t)<0$ và đồ thị hàm số đi lên từ trái qua phải hay hàm số đồng b: $(1 ; e)_{\text {nền }} f^{\prime}(t)>0$.
Từ đó
$$
g^{\prime}(t)-\frac{f^{\prime}(t)(3 t+2019)-3 f(t)}{(3 t+2019)^2}>0
$$
với $t \in(1 ; e)$ hay hàm số $g(t)$ đồng biến trên $(1 ; e)$

Từ BBT ta thây để bất phương trình $m>\frac{f(t)}{3 t+2019}$ với $t \in(1 ; e)$ thì $m>\min _{[1: \mathrm{i}} g(t) \Leftrightarrow m>-\frac{2}{1011}$.
Một chiếc máy bay chuyền động trên đường băng với vận tốc $v(t)-t^2+10 t(\mathrm{~m} / \mathrm{s})$ với $t$ là thời gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyền động. Biết khi máy bay đạt vận tốc $200(\mathrm{~m} / \mathrm{s})$ thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là:
-
$\frac{2500}{3}(\mathrm{~m})$
-
$\frac{4000}{3}(\mathrm{~m})$
-
$500(\mathrm{~m})$
-
$2000(m)$
-
$\frac{2500}{3}(\mathrm{~m})$
-
$\frac{4000}{3}(\mathrm{~m})$
-
$500(\mathrm{~m})$
-
$2000(m)$
Ông Bá Kiến gửi tiết kiệm 100 triệu đồng ở ngân hàng $A$ với lãi suất $6,7 \%$ một năm. Anh giáo Thứ cũng gửi tiết kiệm 20 triệu đồng ở ngân hàng $B$ với lãi suất $7,6 \%$ một năm. Hai người cùng gừi với kì hạn 1 năm theo hịnh thực lãi kép. Hòi sau ít nhất bao nhiêu năm thì tổng số tiền cả vốn lẫn lãi của anh giáo Thứ nhiều hơn số tiền của ông Bá Kiến?
-
192 năm.
-
191 năm.
-
30 năm.
-
31 năm.
-
192 năm.
-
191 năm.
-
30 năm.
-
31 năm.
Tập nghiệm $S$ của bất phương trình $\log _{\frac{1}{2}}\left(\log _3 x\right)>0$ là khoàng $(a ; b)$ . Biều thức $a+b$ bằng
-
4 .
-
3 .
-
$\frac{7}{2}$ .
-
$\frac{5}{2}$
-
4 .
-
3 .
-
$\frac{7}{2}$ .
-
$\frac{5}{2}$
Diện tích hình phẳng giới hạn bời $y=x^2-4 x+3, x=0, x=3$ và trục hoành bằng:
-
$\frac{8}{3}$ .
-
$\frac{1}{3}$ .
-
$\frac{2}{3}$ .
-
$\frac{10}{3}$ .
-
$\frac{8}{3}$ .
-
$\frac{1}{3}$ .
-
$\frac{2}{3}$ .
-
$\frac{10}{3}$ .
Cho hàm số ${ }^{y=\frac{x^3}{3}-(m-1) x^2+3(m-1) x+1}$ . Só giá trị nguyên của $m$ để hàm số đồng biến trên $(1 ;+\infty)$ là:
-
5
-
7
-
4
-
6
-
5
-
7
-
4
-
6
Cho số phức $z=a+b i(a, b \in \mathbb{R})$ theo điều kiện $(2-3 i) z-7 \bar{z}=22-20 i$ . Tính $S=a+b$
-
$S=-4$
-
$S=3$
-
$S=-6$
-
$S=2$
-
$S=-4$
-
$S=3$
-
$S=-6$
-
$S=2$
Trong mặt phẳng $O x y$, tập hợp điểm biểu diễn số phức $z$ thỏa mãn $|z-i|=|2-3 i-z|$ là
-
đường thẳng $x-2 y-3=0$
-
đường thẳng $x+2 y+1=0$
-
đường tròn $x^2+y^2=2$
-
đường thẳng $x^2+y^2=4$
-
đường thẳng $x-2 y-3=0$
-
đường thẳng $x+2 y+1=0$
-
đường tròn $x^2+y^2=2$
-
đường thẳng $x^2+y^2=4$
Trong mặt phẳng với hệ tọa độ $O x y$, cho hình chữ nhật $A B C D$ có diện tích bằng 10 , tâm $I(1 ; 1)$ biết trung điểm $A D$ là $M(0 ;-1)$ . Với $x_D<0$, tọa độ điểm $D$ là
-
$\left(-1 ; \frac{-3}{2}\right)$
-
$\left(-1 ; \frac{1}{2}\right)$
-
$\left(-1 ; \frac{-1}{2}\right)$
-
$\left(-1 ; \frac{3}{2}\right)$
-
$\left(-1 ; \frac{-3}{2}\right)$
-
$\left(-1 ; \frac{1}{2}\right)$
-
$\left(-1 ; \frac{-1}{2}\right)$
-
$\left(-1 ; \frac{3}{2}\right)$
Cho phương trình đường tròn:
$$
x^2+y^2-8 x+10 y+m=0
$$
Điều kiện của $m$ để (*) là phương trình đường tròn có bán kính bằng 7 là:
-
$m=-8$
-
$m=4$
-
$m=8$
-
$m=-4$
-
$m=-8$
-
$m=4$
-
$m=8$
-
$m=-4$
Trong không gian $O x y z$, cho mặt phẳng $(\alpha): 2 x-y+3 z+4=0$ và điểm $A(2 ;-1 ; 2)$ . Mặt phẳng qua $A$ song song với trục $O y$ và vuông góc với ${ }^{(\alpha)}$ có phương trình là:
-
$3 x-2 z-2=0$
-
$-3 x-2 z+10=0$
-
$3 y-2 z-2=0$
-
$3 x-2 z-8=0$
-
$3 x-2 z-2=0$
-
$-3 x-2 z+10=0$
-
$3 y-2 z-2=0$
-
$3 x-2 z-8=0$
Cắt hình nón bời một mặt phẳng qua trục thu được thiết diện là một tam giác vuông có diện tích bằng 8. Diện tích xung quanh của hịhh nón đã cho bằng:
-
$8 \sqrt{2} \pi$
-
$16 \sqrt{2} \pi$
-
$4 \sqrt{2} \pi$
-
$2 \sqrt{2} \pi$
-
$8 \sqrt{2} \pi$
-
$16 \sqrt{2} \pi$
-
$4 \sqrt{2} \pi$
-
$2 \sqrt{2} \pi$
Cho hình nón có chiều cao $h=10$ và bán kính đáy $r=5$ . Xét hình trụ có một đáy nằm trên hình tròn đáy của hỉnh nón, đường tròn đáy còn lại nằm trên mặt xung quanh của hình nón sao cho thể tích khối trụ lớn nhất. Khi đó, bán kính đáy của hình trụ bằng:
-
$\frac{10}{3}$
-
$\frac{5}{2}$
-
$\frac{5}{3}$
-
$\frac{15}{4}$
-
$\frac{10}{3}$
-
$\frac{5}{2}$
-
$\frac{5}{3}$
-
$\frac{15}{4}$
Cho khối lăng trụ tam giác đều $A B C \cdot A^{\prime} B^{\prime} C^{\prime}$ có cạnh đáy là $2 a$ và khoảng cách từ điểm $A$ đến mặt phẳng $\left(A^{\prime} B C\right)$ bằng $a$ . Tính thể tích của khối lăng trụ $A B C \cdot A^{\prime} B^{\prime} C^{\prime}$
-
$\frac{3 a^3 \sqrt{2}}{2}$
-
$\frac{\sqrt{2} a^3}{3}$
-
$\frac{a^3 \sqrt{2}}{2}$
-
$2 \sqrt{2} a^3$
-
$\frac{3 a^3 \sqrt{2}}{2}$
-
$\frac{\sqrt{2} a^3}{3}$
-
$\frac{a^3 \sqrt{2}}{2}$
-
$2 \sqrt{2} a^3$
Cho hình chóp $S . A B C D$ đáy là hình bình hành tâm $O$ . Gọi $M, N, P$ lẩn lượt là trung điểm của $S A, S C, O B$ . Gọi $Q$ là giao điểm của $S D$ với $m p(M N P)$ . Tỉnh $\frac{S Q}{S D}$ .
-
$\frac{S Q}{S D}=\frac{1}{4}$ .
-
$\frac{S Q}{S D}=\frac{1}{3}$ .
-
$\frac{S Q}{S D}=\frac{1}{5}$ .
-
$\frac{S Q}{S D}=\frac{6}{25}$ .
-
$\frac{S Q}{S D}=\frac{1}{4}$ .
-
$\frac{S Q}{S D}=\frac{1}{3}$ .
-
$\frac{S Q}{S D}=\frac{1}{5}$ .
-
$\frac{S Q}{S D}=\frac{6}{25}$ .
Trong không gian $O x y z$, cho hai điểm $A(1 ; 2 ; 3), B(4 ;-7 ;-9)$, tập hợp các điểm $M$ thỏa mãn $2 M A^2+M B^2=165$ là mặt cầu có tâm $I(a ; b ; c)$ và bản kính $R$ . Giá trị biểu thức $T=a^2+b^2+c^2+R^2$ bằng:
-
$T=9$
-
$T=13$
-
$T=15$
-
$T=18$
-
$T=9$
-
$T=13$
-
$T=15$
-
$T=18$
Trong không gian $O x y z$ cho điểm $A(1 ; 1 ;-2)$ và đường thẳng $d: \frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{-2}$ Đường thẳng qua $A$ và song song với $d$ có phương trình tham số là
-
$\left\{\begin{array}{l}x=1+2 t \\ y=1+t \\ z=-2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=1+2 t \\ y=1-t \\ z=-2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=2+t \\ y=1+t \\ z=2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=2+t \\ y=1+t \\ z=-2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=1+2 t \\ y=1+t \\ z=-2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=1+2 t \\ y=1-t \\ z=-2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=2+t \\ y=1+t \\ z=2-2 t\end{array}\right.$
-
$\left\{\begin{array}{l}x=2+t \\ y=1+t \\ z=-2-2 t\end{array}\right.$
Cho hàm số $y=f(x)$ xác định và liên tục trên $\mathbb{R}$, có đồ thị như hình vễ. Hàm số $g(x)=f\left(x^2-2\right)$ có bao nhiêu điểm cực tiểu?

-
3
-
1
-
5
-
2
-
3
-
1
-
5
-
2
Trong không gian $O x y z$, cho hai điểm $A(1 ; 2 ; 3), B(5 ; 6 ; 1)$ . Biết $M(a ; b ; 0)$ sao cho tồng $M A+M B$ nhỏ nhất. Tính độ dài đoạn $O M$ .
-
$O M=\sqrt{41}$
-
$O M=\sqrt{34}$
-
$O M=\sqrt{43}$
-
$O M=\sqrt{14}$
-
$O M=\sqrt{41}$
-
$O M=\sqrt{34}$
-
$O M=\sqrt{43}$
-
$O M=\sqrt{14}$
Gọi $S$ là tập hợp tất cả các giá trị nguyên $m$ để đồ thị hàm số $y=\left|3 x^4-8 x^3-6 x^2+24 x-m\right|$ có 7 điểm cực trị. Tính tổng các phần tử của $S$ .
-
42
-
30
-
50
-
63
-
42
-
30
-
50
-
63
Có bao nhiêu giả trị $m$ nguyên bé hơn -6 để phương trình $\sqrt{2 x^2-2 x-m}=x+2$ có nghiệm?
-
7
-
5
-
6
-
8
-
7
-
5
-
6
-
8
Cho hàm số $y=f(x)$ liên tục trên đoạn $[1 ; 3]$, thỏa mãn $f(4-x)=f(x), \forall x \in[1 ; 3]$ và $\int_1^3 x f(x) d x=-2$ . Giá trị $2 \int_1^3 f(x) d x$ bằng
-
-2
-
1
-
-1
-
2
-
-2
-
1
-
-1
-
2
Một xạ thủ bắn bia. Biết rằng xác suất bắn trúng vòng 10 là 0,$2 ;$ vòng 9 là 0,25 và vòng 8 là 0,15 . Nếu trúng vòng nào thi được số điểm tương ửng với vòng đó. Già sử xạ thủ bắn 3 phát súng một cách độc lập. Xạ thủ đạt loại giòi nếu được ít nhất 28 điểm. Tính xác suất để xạ thủ đạt loại giòi.
-
0,0935
-
0,101
-
0,077
-
0,097
-
0,0935
-
0,101
-
0,077
-
0,097
Cho khối tứ diện $A B C D$ . Gọi $M, N, E$ lần lượt là trung điểm của $A B, B D, D A$ . Tỉ số thể tích của hai khối tứ diện $M N E C$ và $A B C D$ bằng
-
$\frac{1}{4}$
-
$\frac{1}{8}$
-
$\frac{1}{3}$
-
$\frac{1}{2}$
-
$\frac{1}{4}$
-
$\frac{1}{8}$
-
$\frac{1}{3}$
-
$\frac{1}{2}$
Hệ số góc của tiếp tuyến với đồ thị hàm số $y=\ln (x+1)$ tại điểm có hoành độ $x=2$ là
-
$\frac{1}{3}$ .
-
$\frac{1}{4}$ .
-
$\frac{4}{3}$ .
-
$\frac{2}{3}$ .
-
$\frac{1}{3}$ .
-
$\frac{1}{4}$ .
-
$\frac{4}{3}$ .
-
$\frac{2}{3}$ .
Cho hàm số $y=f(x)$ ó́ đạo hàm $f^{\prime}(x)=(\ln x+1)\left(e^x-2019\right)(x+1)$ trên khoàng $(0 ;+\infty)$ . Höi hàm số $y=f(x)$ có bao nhiêu điểm cực trị?
-
2
-
3
-
4
-
0
-
2
-
3
-
4
-
0
Trong không gian với hệ tọa độ $O x y z$, cho hai mặt phẳng $(P): 2 x-y-2 z-9=0$ và $(Q): 4 x-2 y-4 z-6=0$ . Khoảng cách giữa hai mặt phẳng $(P)$ và $(Q)$ bằng
-
2
-
3
-
4
-
0
-
2
-
3
-
4
-
0
Lớp 11A có 15 học sinh nữ, 20 học sinh nam. Có bao nhiêu cách chọn 5 học sinh tham gia văn nghệ trong đó có it nhất 3 học sinh nữ?
-
116753
-
343256
-
236547
-
423132
-
116753
-
343256
-
236547
-
423132
Cho $f(x)$ là một đa thức thóa mãn $\lim _{x \rightarrow 2} \frac{f(x)-15}{x-2}=3$ . Tính
$$
\lim _{x \rightarrow 2} \frac{f(x)-15}{\left(x^2-4\right)(\sqrt{2 f(x)+6}+3)}
$$
-
$\frac{1}{12}$
-
$\frac{1}{2}$
-
$\frac{11}{5}$
-
$\frac{4}{9}$
-
$\frac{1}{12}$
-
$\frac{1}{2}$
-
$\frac{11}{5}$
-
$\frac{4}{9}$
Ký hiệu $M$ và $m$ tương ửng là GTLN và GTNN của hàm số $y=x^2-2 x+5$ trên miền $[2 ; 7]$ . Phát biểu nào sau đây đúng?
-
M = 8m
-
M = 4m
-
M = 2m
-
M = 10m
-
M = 8m
-
M = 4m
-
M = 2m
-
M = 10m
Với tất cả giá trị nào của $m$ thì hàm số $y=m x^4+(m-1) x^2+1-2 m$ chỉ có một cực trị
-
$\left[\begin{array}{l}m \leq 0 \\ m \geq 1\end{array}\right.$
-
$\left[\begin{array}{l}m \leq 3\\ m \geq 5\end{array}\right.$
-
$\left[\begin{array}{l}m \leq -2 \\ m \geq -1\end{array}\right.$
-
$\left[\begin{array}{l}m \leq 2 \\ m \geq 10\end{array}\right.$
– Tính đạo hàm.
– Giải phương trình $y^{\prime}=0$
– Đưa phương trình $y^{\prime}=0$ về dạng tích, tìm điều kiện để phương trình $y^{\prime}=0$ có 1 nghiệm duy nhất.
Giải chi tiết:
+ $y^{\prime}=4 m x^3+2(m-1) x=2 x\left(2 m x^2+m-1\right)$
$+y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}x=0 \\ 2 m x^2+m-1=0(1)\end{array}\right.$
+ Hàm số chi có 1 cực trị $\Leftrightarrow$ (1) vô nghiệm hoặc có nghiệm kép
$$
\Rightarrow \Delta \leq 0 \Leftrightarrow-2 m(m-1) \leq 0 \Leftrightarrow\left[\begin{array}{l}
m \leq 0 \\
m \geq 1
\end{array} .\right.
$$
-
$\left[\begin{array}{l}m \leq 0 \\ m \geq 1\end{array}\right.$
-
$\left[\begin{array}{l}m \leq 3\\ m \geq 5\end{array}\right.$
-
$\left[\begin{array}{l}m \leq -2 \\ m \geq -1\end{array}\right.$
-
$\left[\begin{array}{l}m \leq 2 \\ m \geq 10\end{array}\right.$
– Tính đạo hàm.
– Giải phương trình $y^{\prime}=0$
– Đưa phương trình $y^{\prime}=0$ về dạng tích, tìm điều kiện để phương trình $y^{\prime}=0$ có 1 nghiệm duy nhất.
Giải chi tiết:
+ $y^{\prime}=4 m x^3+2(m-1) x=2 x\left(2 m x^2+m-1\right)$
$+y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}x=0 \\ 2 m x^2+m-1=0(1)\end{array}\right.$
+ Hàm số chi có 1 cực trị $\Leftrightarrow$ (1) vô nghiệm hoặc có nghiệm kép
$$
\Rightarrow \Delta \leq 0 \Leftrightarrow-2 m(m-1) \leq 0 \Leftrightarrow\left[\begin{array}{l}
m \leq 0 \\
m \geq 1
\end{array} .\right.
$$
Diện tích hình phẳng giới hạn bời đồ thị hàm số $y=x^2-4 x+3$, trục hoành và hai đường thẳng $x=1, x=2$ bằng:
-
${ }^{\frac{2}{3}}$
-
${ }^{\frac{1}{3}}$
-
${ }^{\frac{5}{3}}$
-
${ }^{\frac{10}{3}}$
-
${ }^{\frac{2}{3}}$
-
${ }^{\frac{1}{3}}$
-
${ }^{\frac{5}{3}}$
-
${ }^{\frac{10}{3}}$
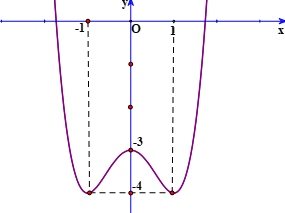
Cho hàm số $y=f(x)$ có đồ thị như hình vẽ sau. Tìm $m$ để phương trình $f(\sin x)=m$ có đúng hai nghiệm trên đoạn $[0 ; \pi]$ .
-
$-4
-
$-1
-
$-4
-
$0
-
$-4
-
$-1
-
$-4
-
$0
Với số phức $z$ thỏa mãn $|z-2+i|=4$, tập hợp các điểm biểu diễn các số phức $z$ là một đường tròn. Tìm bán kính $R$ của đường tròn đó.
-
$R=4$
-
$R=2$
-
$R=0$
-
$R=-1$
-
$R=4$
-
$R=2$
-
$R=0$
-
$R=-1$
Cho lăng trụ đều $A B C \cdot A^{\prime} B^{\prime} C^{\prime}$ có tất cả các cạnh bằng $a$ . Gọi $\alpha$ là góc giữa mặt phẳng $\left(A^{\prime} B C\right)$ và mặt phẳng $(A B C)$ . Tính $\tan \alpha$ .
-
$\tan \alpha=\frac{2 \sqrt{3}}{3}$
-
$\tan \alpha=\frac{4 \sqrt{3}}{3}$
-
$\tan \alpha=\frac{\sqrt{3}}{2}$
-
$\tan \alpha=\frac{\sqrt{3}}{3}$
-
$\tan \alpha=\frac{2 \sqrt{3}}{3}$
-
$\tan \alpha=\frac{4 \sqrt{3}}{3}$
-
$\tan \alpha=\frac{\sqrt{3}}{2}$
-
$\tan \alpha=\frac{\sqrt{3}}{3}$
Trong không gian với hệ tọa độ $O x y z$, tìm tọa độ điểm $A^{\prime}$ đối xứng với điểm $A(-1 ; 0 ; 3)$ qua mặt phẳng $(P): x+3 y-2 z-7=0$ .
-
$A^{\prime}(1 ; 6 ;-1)$
-
$A^{\prime}(1 ; 3 ;-1)$
-
$A^{\prime}(-1 ; -6 ;-1)$
-
$A^{\prime}(0 ; -6 ; 1)$
-
$A^{\prime}(1 ; 6 ;-1)$
-
$A^{\prime}(1 ; 3 ;-1)$
-
$A^{\prime}(-1 ; -6 ;-1)$
-
$A^{\prime}(0 ; -6 ; 1)$
Xét các số thực $x, y$ thỏa mãn $2^{x^2+y^2+1} \leq\left(x^2+y^2-2 x+2\right) 4^x$ . Giả trị lớn nhất của biểu thức $P=\frac{8 x+4}{2 x-y+1}$ gần nhất với số nào dưới đây?
-
7
-
3
-
2
-
1
-
7
-
3
-
2
-
1
Cho hình chóp $S . A B C D$ có đáy là hình vuông cạnh $2 a$, tam giác $S A B$ cân tại $S$ và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng $(S C D)$ và $(A B C D)$ bằng $\varphi$ và $\sin \varphi=\frac{\sqrt{5}}{5}$ . Khoàng cách từ điểm $A$ đến mặt phẳng $(S C D)$ bằng:
-
$\frac{2 \sqrt{5} a}{5}$
-
$\frac{\sqrt{5} a}{5}$
-
$\frac{2 \sqrt{3} a}{3}$
-
$\frac{\sqrt{2} a}{2}$
-
$\frac{2 \sqrt{5} a}{5}$
-
$\frac{\sqrt{5} a}{5}$
-
$\frac{2 \sqrt{3} a}{3}$
-
$\frac{\sqrt{2} a}{2}$
Ông $A$ dự định sử dụng hết $6,5 \mathrm{~m}^3$ kinh đề làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều đài gấp đôi chiều rộng (các mối ghép có kich thước không đáng kể). Bể cá có đung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
-
$1,50 \mathrm{~m}^3$
-
$1,05 \mathrm{~m}^3$
-
$0,87 \mathrm{~m}^3$
-
$1,34 \mathrm{~m}^3$
– Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là $x, 2 x, y$
– Tìm mối liên hệ $x, y$ dựa vào dữ kiện diện tích $6,5 m^2$ .
– Lập hàm số thể tich theo ẩn $x$ và xét hàm tìm $V_{\max }$ .
Giải chi tiết:
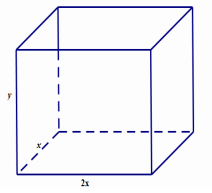
Gọi chiều rộng, chiều đài, chiều cao của bể lần lượt là $x, 2 x, y(x, y>0)$
Diện tích phần lắp kính là: $2 x x+2 x y+2 \cdot 2 x \cdot y=2 x^2+6 x y=6,5$
$$
\Leftrightarrow x y=\frac{6,5-2 x^2}{6}>0 \Rightarrow x<\sqrt{\frac{6,5}{2}}=\frac{\sqrt{13}}{2} \text {. }
$$
Thể tích bể cá là:
$$
V=2 x x, y=2 x, \frac{6,5-2 x^2}{6}=\frac{-4 x^3+13 x}{6} \quad 0<x<\frac{\sqrt{13}}{2}
$$
Ta có:
$$
V^{\prime}=\frac{-12 x^2+13}{6}, V^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}
x=\frac{\sqrt{39}}{6} \\
x=-\frac{\sqrt{39}}{6}(L)
\end{array}\right.
$$
Bảng biến thiên:
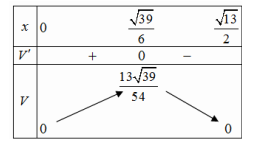
Vậy
$$
V_{\max }=\frac{13 \sqrt{39}}{54} \approx 1,50 \mathrm{~m}^3
$$
-
$1,50 \mathrm{~m}^3$
-
$1,05 \mathrm{~m}^3$
-
$0,87 \mathrm{~m}^3$
-
$1,34 \mathrm{~m}^3$
– Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là $x, 2 x, y$
– Tìm mối liên hệ $x, y$ dựa vào dữ kiện diện tích $6,5 m^2$ .
– Lập hàm số thể tich theo ẩn $x$ và xét hàm tìm $V_{\max }$ .
Giải chi tiết:

Gọi chiều rộng, chiều đài, chiều cao của bể lần lượt là $x, 2 x, y(x, y>0)$
Diện tích phần lắp kính là: $2 x x+2 x y+2 \cdot 2 x \cdot y=2 x^2+6 x y=6,5$
$$
\Leftrightarrow x y=\frac{6,5-2 x^2}{6}>0 \Rightarrow x<\sqrt{\frac{6,5}{2}}=\frac{\sqrt{13}}{2} \text {. }
$$
Thể tích bể cá là:
$$
V=2 x x, y=2 x, \frac{6,5-2 x^2}{6}=\frac{-4 x^3+13 x}{6} \quad 0<x<\frac{\sqrt{13}}{2}
$$
Ta có:
$$
V^{\prime}=\frac{-12 x^2+13}{6}, V^{\prime}=0 \Leftrightarrow\left[\begin{array}{l}
x=\frac{\sqrt{39}}{6} \\
x=-\frac{\sqrt{39}}{6}(L)
\end{array}\right.
$$
Bảng biến thiên:

Vậy
$$
V_{\max }=\frac{13 \sqrt{39}}{54} \approx 1,50 \mathrm{~m}^3
$$
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như có thể một lúc nào, biết đâu A Phủ chẳng trốn được rồi, lúc đó bố con thống lý sẽ đổ là Mị đã cởi trói cho nó, Mị liền phải trói thay vào đấy. Mị chết trên cái cọc ấy. Nghĩ thế, nhưng làm sao Mị cũng không thấy sợ…Trong nhà tối bưng, Mị rón rén bước lại, A Phủ vẫn nhắm mắt. Nhưng Mị tưởng như A Phủ biết có người bước lại… Mị rút con dao nhỏ cắt lúa, cắt nút dây mây. A Phủ thở phè từng hơi, như rắn thở, không biết mê hay tỉnh.Lần lần, đến lúc gỡ được hết dây trói ở người A Phủ thì Mị cũng hốt hoảng. Mị chỉ thì thào được một tiếng “Đi đi…” rồi Mị nghẹn lại. A Phủ khuỵu xuống không bước nổi. Nhưng trước cái chết có thể đến nơi ngay, A Phủ lại quật sức vùng lên, chạy.
Mị đứng lặng trong bóng tối.
Trời tối lắm. Mị vẫn băng đi. Mỵ đuổi kịp A Phủ, đã lăn, chạy xuống tới lưng dốc.
(Trích Vợ chồng A Phủ của Tô Hoài, SGK Ngữ văn lớp 12, tập 2)
Nội dung chủ yếu của đoạn văn bản là gì?
-
Thể hiện tâm trạng và hành động của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện hành động của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện tâm trạng của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện niềm tin của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
Nội dung đoạn trích thể hiện tâm trạng và hành động của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện tâm trạng và hành động của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện hành động của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện tâm trạng của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
-
Thể hiện niềm tin của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
Nội dung đoạn trích thể hiện tâm trạng và hành động của nhân vật Mị trong đêm cởi trói cho A Phủ và cùng A Phủ trốn khỏi Hồng Ngài sang Phiềng Sa.
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như có thể một lúc nào, biết đâu A Phủ chẳng trốn được rồi, lúc đó bố con thống lý sẽ đổ là Mị đã cởi trói cho nó, Mị liền phải trói thay vào đấy. Mị chết trên cái cọc ấy. Nghĩ thế, nhưng làm sao Mị cũng không thấy sợ…Trong nhà tối bưng, Mị rón rén bước lại, A Phủ vẫn nhắm mắt. Nhưng Mị tưởng như A Phủ biết có người bước lại… Mị rút con dao nhỏ cắt lúa, cắt nút dây mây. A Phủ thở phè từng hơi, như rắn thở, không biết mê hay tỉnh.Lần lần, đến lúc gỡ được hết dây trói ở người A Phủ thì Mị cũng hốt hoảng. Mị chỉ thì thào được một tiếng “Đi đi…” rồi Mị nghẹn lại. A Phủ khuỵu xuống không bước nổi. Nhưng trước cái chết có thể đến nơi ngay, A Phủ lại quật sức vùng lên, chạy.
Mị đứng lặng trong bóng tối.
Trời tối lắm. Mị vẫn băng đi. Mỵ đuổi kịp A Phủ, đã lăn, chạy xuống tới lưng dốc.
(Trích Vợ chồng A Phủ của Tô Hoài, SGK Ngữ văn lớp 12, tập 2)
Nêu ý nghĩa của đoạn văn trên.
-
Cả ba đáp án trên đều đúng.
-
Niềm khát khao sống và khát khao tự do của nhân vật Mị.
-
Thể hiện sức sống tiềm tàng của nhân vật: Mị cứu A Phủ cũng đồng nghĩa với việc Mị tự cứu lấy chính bản thân mình.
-
Ca ngợi những phẩm chất đẹp đẽ của người phụ nữ miền núi nói riêng và những người phụ nữ Việt Nam nói chung.
-
Cả ba đáp án trên đều đúng.
-
Niềm khát khao sống và khát khao tự do của nhân vật Mị.
-
Thể hiện sức sống tiềm tàng của nhân vật: Mị cứu A Phủ cũng đồng nghĩa với việc Mị tự cứu lấy chính bản thân mình.
-
Ca ngợi những phẩm chất đẹp đẽ của người phụ nữ miền núi nói riêng và những người phụ nữ Việt Nam nói chung.
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như có thể một lúc nào, biết đâu A Phủ chẳng trốn được rồi, lúc đó bố con thống lý sẽ đổ là Mị đã cởi trói cho nó, Mị liền phải trói thay vào đấy. Mị chết trên cái cọc ấy. Nghĩ thế, nhưng làm sao Mị cũng không thấy sợ…Trong nhà tối bưng, Mị rón rén bước lại, A Phủ vẫn nhắm mắt. Nhưng Mị tưởng như A Phủ biết có người bước lại… Mị rút con dao nhỏ cắt lúa, cắt nút dây mây. A Phủ thở phè từng hơi, như rắn thở, không biết mê hay tỉnh.Lần lần, đến lúc gỡ được hết dây trói ở người A Phủ thì Mị cũng hốt hoảng. Mị chỉ thì thào được một tiếng “Đi đi…” rồi Mị nghẹn lại. A Phủ khuỵu xuống không bước nổi. Nhưng trước cái chết có thể đến nơi ngay, A Phủ lại quật sức vùng lên, chạy.
Mị đứng lặng trong bóng tối.
Trời tối lắm. Mị vẫn băng đi. Mỵ đuổi kịp A Phủ, đã lăn, chạy xuống tới lưng dốc.
(Trích Vợ chồng A Phủ của Tô Hoài, SGK Ngữ văn lớp 12, tập 2)
Xác định ý nghĩa nghệ thuật của hình ảnh cái cọc và dây mây trong văn bản ?
-
Ý nghĩa tả thực, ý nghĩa tượng trưng
-
Ý nghĩa tả thực
-
Ý nghĩa tượng trưng
-
Không mang ý nghĩa
-
Ý nghĩa tả thực, ý nghĩa tượng trưng
-
Ý nghĩa tả thực
-
Ý nghĩa tượng trưng
-
Không mang ý nghĩa
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như có thể một lúc nào, biết đâu A Phủ chẳng trốn được rồi, lúc đó bố con thống lý sẽ đổ là Mị đã cởi trói cho nó, Mị liền phải trói thay vào đấy. Mị chết trên cái cọc ấy. Nghĩ thế, nhưng làm sao Mị cũng không thấy sợ…Trong nhà tối bưng, Mị rón rén bước lại, A Phủ vẫn nhắm mắt. Nhưng Mị tưởng như A Phủ biết có người bước lại… Mị rút con dao nhỏ cắt lúa, cắt nút dây mây. A Phủ thở phè từng hơi, như rắn thở, không biết mê hay tỉnh.Lần lần, đến lúc gỡ được hết dây trói ở người A Phủ thì Mị cũng hốt hoảng. Mị chỉ thì thào được một tiếng “Đi đi…” rồi Mị nghẹn lại. A Phủ khuỵu xuống không bước nổi. Nhưng trước cái chết có thể đến nơi ngay, A Phủ lại quật sức vùng lên, chạy.
Mị đứng lặng trong bóng tối.
Trời tối lắm. Mị vẫn băng đi. Mỵ đuổi kịp A Phủ, đã lăn, chạy xuống tới lưng dốc.
(Trích Vợ chồng A Phủ của Tô Hoài, SGK Ngữ văn lớp 12, tập 2)
Phương thức biểu đạt chính trong đoạn trích là gì?
-
Phương thức biểu đạt tự sự
-
Phương thức biểu đạt nghị luận
-
Phương thức biểu đạt miêu tả
-
Phương thức biểu đạt biểu cảm
-
Phương thức biểu đạt tự sự
-
Phương thức biểu đạt nghị luận
-
Phương thức biểu đạt miêu tả
-
Phương thức biểu đạt biểu cảm
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như có thể một lúc nào, biết đâu A Phủ chẳng trốn được rồi, lúc đó bố con thống lý sẽ đổ là Mị đã cởi trói cho nó, Mị liền phải trói thay vào đấy. Mị chết trên cái cọc ấy. Nghĩ thế, nhưng làm sao Mị cũng không thấy sợ…Trong nhà tối bưng, Mị rón rén bước lại, A Phủ vẫn nhắm mắt. Nhưng Mị tưởng như A Phủ biết có người bước lại… Mị rút con dao nhỏ cắt lúa, cắt nút dây mây. A Phủ thở phè từng hơi, như rắn thở, không biết mê hay tỉnh.Lần lần, đến lúc gỡ được hết dây trói ở người A Phủ thì Mị cũng hốt hoảng. Mị chỉ thì thào được một tiếng “Đi đi…” rồi Mị nghẹn lại. A Phủ khuỵu xuống không bước nổi. Nhưng trước cái chết có thể đến nơi ngay, A Phủ lại quật sức vùng lên, chạy.
Mị đứng lặng trong bóng tối.
Trời tối lắm. Mị vẫn băng đi. Mỵ đuổi kịp A Phủ, đã lăn, chạy xuống tới lưng dốc.
(Trích Vợ chồng A Phủ của Tô Hoài, SGK Ngữ văn lớp 12, tập 2)
Các từ láy được tác giả sử dụng trong đoạn thơ trên:
-
rón rén, hốt hoảng, thì thào
-
rón rén, nhắm mắt, thì thào
-
rón rén, khuỵu xuống, hốt hoảng
-
hốt hoảng, thì thào
-
rón rén, hốt hoảng, thì thào
-
rón rén, nhắm mắt, thì thào
-
rón rén, khuỵu xuống, hốt hoảng
-
hốt hoảng, thì thào
Mỗi người trên thế giới đều là những người khách bộ hành, mỗi ngày đều bước đi một cách chủ động hoặc bị động trên con đường mình đã chọn…..
Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh. Bất luận gian khổ thế nào, chỉ cần chúng ta còn sống, chúng ta còn phải đối mặt. Sống tức là thực hiện một cuộc hành trình không thể trì hoãn….
Trước muôn vàn lối rẽ, không ai có được bản đồ trong tay, cũng không phải ai cũng có kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân. Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.
(Trích Bí quyết thành công của BillGates, Khẩm Sài Nhân, NXB Hồng Đức)
Xác định phong cách ngôn ngữ của đoạn văn bản trên.
-
Phong cách ngôn ngữ báo chí
-
Phong cách ngôn ngữ sinh hoạt
-
Phong cách ngôn ngữ chính luận
-
Phong cách ngôn ngữ nghệ thuật
-
Phong cách ngôn ngữ báo chí
-
Phong cách ngôn ngữ sinh hoạt
-
Phong cách ngôn ngữ chính luận
-
Phong cách ngôn ngữ nghệ thuật
Mỗi người trên thế giới đều là những người khách bộ hành, mỗi ngày đều bước đi một cách chủ động hoặc bị động trên con đường mình đã chọn…..
Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh. Bất luận gian khổ thế nào, chỉ cần chúng ta còn sống, chúng ta còn phải đối mặt. Sống tức là thực hiện một cuộc hành trình không thể trì hoãn….
Trước muôn vàn lối rẽ, không ai có được bản đồ trong tay, cũng không phải ai cũng có kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân. Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.
(Trích Bí quyết thành công của BillGates, Khẩm Sài Nhân, NXB Hồng Đức)
Chỉ ra biện pháp tu từ chính được sử dụng trong câu: “Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh”.
-
Liệt kê
-
Hoán dụ
-
Nhân hóa
-
Đảo ngữ
-
Liệt kê
-
Hoán dụ
-
Nhân hóa
-
Đảo ngữ
Mỗi người trên thế giới đều là những người khách bộ hành, mỗi ngày đều bước đi một cách chủ động hoặc bị động trên con đường mình đã chọn…..
Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh. Bất luận gian khổ thế nào, chỉ cần chúng ta còn sống, chúng ta còn phải đối mặt. Sống tức là thực hiện một cuộc hành trình không thể trì hoãn….
Trước muôn vàn lối rẽ, không ai có được bản đồ trong tay, cũng không phải ai cũng có kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân. Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.
(Trích Bí quyết thành công của BillGates, Khẩm Sài Nhân, NXB Hồng Đức)
Anh/Chị hiểu như thế nào về câu nói: “Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.”
-
Trong cuộc sống nếu ta lựa chọn sai hướng đi sẽ khó có thể đi đến thành công, ngược lại nếu có quyết định lựa chọn đúng đắn sẽ mang đến những kết quả, thành công tốt đẹp.
-
Cuộc sống không phải bao giờ cũng thuận lợi, suôn sẻ, mà luôn có những khó khăn, thử thách
Vì vậy mỗi người cần trân trọng những phút giây mình đang có.
-
Cuộc sống có muôn vàn khó khăn thử thách, chúng ta không thể chọn cách trốn tránh mãi được mà cần phải đối mặt, đương đầu để vượt qua.
-
Trong cuộc đời sẽ phải trải qua rất nhiều khó khăn, vấp ngã, thậm chí thất bại nhưng khi còn sống, còn hơi thở thì ta không ngừng nỗ lực, cố gắng.
-
Trong cuộc sống nếu ta lựa chọn sai hướng đi sẽ khó có thể đi đến thành công, ngược lại nếu có quyết định lựa chọn đúng đắn sẽ mang đến những kết quả, thành công tốt đẹp.
-
Cuộc sống không phải bao giờ cũng thuận lợi, suôn sẻ, mà luôn có những khó khăn, thử thách
Vì vậy mỗi người cần trân trọng những phút giây mình đang có. -
Cuộc sống có muôn vàn khó khăn thử thách, chúng ta không thể chọn cách trốn tránh mãi được mà cần phải đối mặt, đương đầu để vượt qua.
-
Trong cuộc đời sẽ phải trải qua rất nhiều khó khăn, vấp ngã, thậm chí thất bại nhưng khi còn sống, còn hơi thở thì ta không ngừng nỗ lực, cố gắng.
Mỗi người trên thế giới đều là những người khách bộ hành, mỗi ngày đều bước đi một cách chủ động hoặc bị động trên con đường mình đã chọn…..
Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh. Bất luận gian khổ thế nào, chỉ cần chúng ta còn sống, chúng ta còn phải đối mặt. Sống tức là thực hiện một cuộc hành trình không thể trì hoãn….
Trước muôn vàn lối rẽ, không ai có được bản đồ trong tay, cũng không phải ai cũng có kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân. Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.
(Trích Bí quyết thành công của BillGates, Khẩm Sài Nhân, NXB Hồng Đức)
Phương thức biểu đạt chính trong đoạn trích là gì?
-
Phương thức biểu đạt nghị luận
-
Phương thức biểu đạt tự sự
-
Phương thức biểu đạt miêu tả
-
Phương thức biểu đạt biểu cảm
-
Phương thức biểu đạt nghị luận
-
Phương thức biểu đạt tự sự
-
Phương thức biểu đạt miêu tả
-
Phương thức biểu đạt biểu cảm
Mỗi người trên thế giới đều là những người khách bộ hành, mỗi ngày đều bước đi một cách chủ động hoặc bị động trên con đường mình đã chọn…..
Cuộc đời không chỉ là con đường đi khó, đôi khi chúng ta còn gặp phải những hố sâu do người khác tạo ra, gặp phải sự tấn công của thú dữ, mưa bão và tuyết lạnh. Bất luận gian khổ thế nào, chỉ cần chúng ta còn sống, chúng ta còn phải đối mặt. Sống tức là thực hiện một cuộc hành trình không thể trì hoãn….
Trước muôn vàn lối rẽ, không ai có được bản đồ trong tay, cũng không phải ai cũng có kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân. Nếu bạn rẽ nhầm lối, khoảng cách với xuất phát điểm sẽ bị rút ngắn ngược lại, nếu rẽ đúng, con đường phía trước sẽ bằng phẳng, rộng rãi.
(Trích Bí quyết thành công của BillGates, Khẩm Sài Nhân, NXB Hồng Đức)
Theo tác giả, mỗi người trên thế giới này được liên tưởng với điều gì?
-
Mỗi người trên thế giới được liên tưởng với những người khách bộ hành đi trên con đường mà mình đã chọn.
-
Mỗi người trên thế giới được liên tưởng với những những hố sâu do người khác tạo ra.
-
Mỗi người trên thế giới được liên tưởng với thú dữ, mưa bão và tuyết lạnh
-
Mỗi người trên thế giới được liên tưởng với những kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân.
-
Mỗi người trên thế giới được liên tưởng với những người khách bộ hành đi trên con đường mà mình đã chọn.
-
Mỗi người trên thế giới được liên tưởng với những những hố sâu do người khác tạo ra.
-
Mỗi người trên thế giới được liên tưởng với thú dữ, mưa bão và tuyết lạnh
-
Mỗi người trên thế giới được liên tưởng với những kim chỉ nam dẫn đường, tất cả đều phải dựa vào phán đoán và lựa chọn của bản thân.
Dù đục, dù trong con sông vẫn chảy
Dù cao, dù thấp cây lá vẫn xanh
Dù người phàm tục hay kẻ tu hành
Đều phải sống từ những điều rất nhỏ.
Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm?
Đất ấp ôm cho muôn hạt nảy mầm
Những chồi non tự vươn lên tìm ánh sáng
Nếu tất cả đường đời đều trơn láng
Chắc gì ta đã nhận ra ta
Ai trong đời cũng có thể tiến xa
Nếu có khả năng tự mình đứng dậy.
Hạnh phúc cũng như bầu trời này vậy
Đâu chỉ dành cho một riêng ai.
(Tự sự – Lưu Quang Vũ)
Ý nào sau đây KHÔNG nêu được ý nghĩa của bài thơ?
-
Bản chất cuộc đời là không đơn giản, là một ngã rẽ.
-
Con người có trải qua thử thách mới hiểu rõ chính mình và trưởng thành hơn.
-
Muốn có được hạnh phúc phải tự mình nỗ lực vươn lên.
-
Cần biết nâng niu, trân trọng những cái nhỏ bé trong cuộc sống thì mới có được hạnh phúc lớn lao.
-
Bản chất cuộc đời là không đơn giản, là một ngã rẽ.
-
Con người có trải qua thử thách mới hiểu rõ chính mình và trưởng thành hơn.
-
Muốn có được hạnh phúc phải tự mình nỗ lực vươn lên.
-
Cần biết nâng niu, trân trọng những cái nhỏ bé trong cuộc sống thì mới có được hạnh phúc lớn lao.
Dù đục, dù trong con sông vẫn chảy
Dù cao, dù thấp cây lá vẫn xanh
Dù người phàm tục hay kẻ tu hành
Đều phải sống từ những điều rất nhỏ.
Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm?
Đất ấp ôm cho muôn hạt nảy mầm
Những chồi non tự vươn lên tìm ánh sáng
Nếu tất cả đường đời đều trơn láng
Chắc gì ta đã nhận ra ta
Ai trong đời cũng có thể tiến xa
Nếu có khả năng tự mình đứng dậy.
Hạnh phúc cũng như bầu trời này vậy
Đâu chỉ dành cho một riêng ai.
(Tự sự – Lưu Quang Vũ)
Phương thức biểu đạt nào sau đây KHÔNG được sử dụng trong bài?
-
Phương thức biểu đạt miêu tả
-
Phương thức biểu đạt biểu cảm
-
Phương thức biểu đạt nghị luận
-
Phương thức biểu đạt nghị luận và biểu cảm
-
Phương thức biểu đạt miêu tả
-
Phương thức biểu đạt biểu cảm
-
Phương thức biểu đạt nghị luận
-
Phương thức biểu đạt nghị luận và biểu cảm
Dù đục, dù trong con sông vẫn chảy
Dù cao, dù thấp cây lá vẫn xanh
Dù người phàm tục hay kẻ tu hành
Đều phải sống từ những điều rất nhỏ.
Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm?
Đất ấp ôm cho muôn hạt nảy mầm
Những chồi non tự vươn lên tìm ánh sáng
Nếu tất cả đường đời đều trơn láng
Chắc gì ta đã nhận ra ta
Ai trong đời cũng có thể tiến xa
Nếu có khả năng tự mình đứng dậy.
Hạnh phúc cũng như bầu trời này vậy
Đâu chỉ dành cho một riêng ai.
(Tự sự – Lưu Quang Vũ)
Chỉ ra biện pháp tu từ được sử dụng trong khổ thơ đầu của văn bản:
Dù đục, dù trong con sông vẫn chảy
Dù cao, dù thấp cây lá vẫn xanh
Dù người phàm tục hay kẻ tu hành
Đều phải sống từ những điều rất nhỏ.
-
Điệp ngữ, đối lập, liệt kê
-
Nhân hóa, ẩn dụ
-
Điệp ngữ, so sánh
-
Nhân hóa, đối lập, điệp ngữ
-
Điệp ngữ, đối lập, liệt kê
-
Nhân hóa, ẩn dụ
-
Điệp ngữ, so sánh
-
Nhân hóa, đối lập, điệp ngữ
Dù đục, dù trong con sông vẫn chảy
Dù cao, dù thấp cây lá vẫn xanh
Dù người phàm tục hay kẻ tu hành
Đều phải sống từ những điều rất nhỏ.
Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm?
Đất ấp ôm cho muôn hạt nảy mầm
Những chồi non tự vươn lên tìm ánh sáng
Nếu tất cả đường đời đều trơn láng
Chắc gì ta đã nhận ra ta
Ai trong đời cũng có thể tiến xa
Nếu có khả năng tự mình đứng dậy.
Hạnh phúc cũng như bầu trời này vậy
Đâu chỉ dành cho một riêng ai.
(Tự sự – Lưu Quang Vũ)
Hình ảnh “đường đời trơn láng” đã thể hiện điều gì?
-
Cuộc sống quá bằng phẳng, yên ổn, không có trở ngại, khó khăn.
-
Không gục ngã trước khó khăn, trước phi lý bất công.
-
Cuộc sống có nhiều khó khăn, trở ngại.
-
Cuộc sống phải biết chấp nhận, biết nhìn đời bằng con mắt lạc quan.
-
Cuộc sống quá bằng phẳng, yên ổn, không có trở ngại, khó khăn.
-
Không gục ngã trước khó khăn, trước phi lý bất công.
-
Cuộc sống có nhiều khó khăn, trở ngại.
-
Cuộc sống phải biết chấp nhận, biết nhìn đời bằng con mắt lạc quan.
Dù đục, dù trong con sông vẫn chảy
Dù cao, dù thấp cây lá vẫn xanh
Dù người phàm tục hay kẻ tu hành
Đều phải sống từ những điều rất nhỏ.
Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm?
Đất ấp ôm cho muôn hạt nảy mầm
Những chồi non tự vươn lên tìm ánh sáng
Nếu tất cả đường đời đều trơn láng
Chắc gì ta đã nhận ra ta
Ai trong đời cũng có thể tiến xa
Nếu có khả năng tự mình đứng dậy.
Hạnh phúc cũng như bầu trời này vậy
Đâu chỉ dành cho một riêng ai.
(Tự sự – Lưu Quang Vũ)
Nêu ý nghĩa của hai câu thơ:
“Ta hay chê rằng cuộc đời méo mó
Sao ta không tròn ngay tự trong tâm”
-
Khi đứng trước cái “méo mó” của nhân sinh, cần có thái độ tích cực, chủ động, lạc quan.
-
Con người có trải qua thử thách mới chinh phục được đến đích.
-
Cuộc sống có nhiều khó khăn, trở ngại.
-
Cuộc sống biết cho đi thì mới được nhận lại
-
Khi đứng trước cái “méo mó” của nhân sinh, cần có thái độ tích cực, chủ động, lạc quan.
-
Con người có trải qua thử thách mới chinh phục được đến đích.
-
Cuộc sống có nhiều khó khăn, trở ngại.
-
Cuộc sống biết cho đi thì mới được nhận lại
(1) Một lần tình cờ tôi đọc được bài viết “Hạnh phúc là gì?” trên blốc của một người bạn. (2) Bạn ấy viết rằng: “Hạnh phúc là được nằm trong chăn ấm xem ti vi cùng với gia đình. (3) Hạnh phúc là được trùm chăn kín và được mẹ pha cho cốc sữa nóng. (4) Hạnh phúc là được cùng đứa bạn thân nhong nhong trên khắp phố. (5) Hạnh phúc là ngồi co ro hàng giờ trong quán cà phê, nhấm nháp li ca-cao nóng và bàn chuyện chiến sự… thế giới cùng anh em chiến hữu…”.
(6) Bất chợt giật mình, hạnh phúc đơn giản vậy sao? (7) Ừ nhỉ! (8) Dường như lâu nay chúng ta chỉ quen với việc than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc. (9) Hãy một lần thử nghĩ xem: Khi chúng ta than phiền
Vì bố mẹ quá quan tâm đến chuyện của mình thì ngoài kia biết bao nhiêu người thèm hơi ấm của mẹ, thèm tiếng cười của bố, thèm được về nhà để được mắng; khi chúng ta cảm thấy thiệt thòi khi không được ngồi xe hơi chỉ
Vì phải chạy xe máy giữa trời nắng thì ngoài kia biết bao nhiêu bạn của chúng ta mồ hôi nhễ nhại, gò mình đạp xe lên những con dốc vắng; khi chúng ta bất mãn với chuyện học hành quá căng thẳng thì ngoài kia biết bao người đang khao khát một lần được đến trường, một lần được cầm cây bút để viết lên những ước mơ; khi chúng ta…
(Dẫn theo Bài tập Ngữ văn 11, tập 2, NXB Giáo dục 2007)
Nội dung chính của văn bản trên là gì?
-
Nói về những hạnh phúc bình dị, đơn giản nhưng thiết thực trong cuộc sống
-
Nói về hạnh phúc là hài hòa giữa lợi ích của cá nhân và cộng đồn
-
Nói về hiện tượng “than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc”.
-
Nói về hạnh phúc là một trạng thái tâm lý của con người
-
Nói về những hạnh phúc bình dị, đơn giản nhưng thiết thực trong cuộc sống
-
Nói về hạnh phúc là hài hòa giữa lợi ích của cá nhân và cộng đồn
-
Nói về hiện tượng “than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc”.
-
Nói về hạnh phúc là một trạng thái tâm lý của con người
(1) Một lần tình cờ tôi đọc được bài viết “Hạnh phúc là gì?” trên blốc của một người bạn. (2) Bạn ấy viết rằng: “Hạnh phúc là được nằm trong chăn ấm xem ti vi cùng với gia đình. (3) Hạnh phúc là được trùm chăn kín và được mẹ pha cho cốc sữa nóng. (4) Hạnh phúc là được cùng đứa bạn thân nhong nhong trên khắp phố. (5) Hạnh phúc là ngồi co ro hàng giờ trong quán cà phê, nhấm nháp li ca-cao nóng và bàn chuyện chiến sự… thế giới cùng anh em chiến hữu…”.
(6) Bất chợt giật mình, hạnh phúc đơn giản vậy sao? (7) Ừ nhỉ! (8) Dường như lâu nay chúng ta chỉ quen với việc than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc. (9) Hãy một lần thử nghĩ xem: Khi chúng ta than phiền
Vì bố mẹ quá quan tâm đến chuyện của mình thì ngoài kia biết bao nhiêu người thèm hơi ấm của mẹ, thèm tiếng cười của bố, thèm được về nhà để được mắng; khi chúng ta cảm thấy thiệt thòi khi không được ngồi xe hơi chỉ
Vì phải chạy xe máy giữa trời nắng thì ngoài kia biết bao nhiêu bạn của chúng ta mồ hôi nhễ nhại, gò mình đạp xe lên những con dốc vắng; khi chúng ta bất mãn với chuyện học hành quá căng thẳng thì ngoài kia biết bao người đang khao khát một lần được đến trường, một lần được cầm cây bút để viết lên những ước mơ; khi chúng ta…
(Dẫn theo Bài tập Ngữ văn 11, tập 2, NXB Giáo dục 2007)
Xác định phong cách ngôn ngữ của đoạn văn bản trên.
-
Phong cách ngôn ngữ chính luận
-
Phong cách ngôn ngữ sinh hoạt
-
Phong cách ngôn ngữ báo chí
-
Phong cách ngôn ngữ nghệ thuật
-
Phong cách ngôn ngữ chính luận
-
Phong cách ngôn ngữ sinh hoạt
-
Phong cách ngôn ngữ báo chí
-
Phong cách ngôn ngữ nghệ thuật
(1) Một lần tình cờ tôi đọc được bài viết “Hạnh phúc là gì?” trên blốc của một người bạn. (2) Bạn ấy viết rằng: “Hạnh phúc là được nằm trong chăn ấm xem ti vi cùng với gia đình. (3) Hạnh phúc là được trùm chăn kín và được mẹ pha cho cốc sữa nóng. (4) Hạnh phúc là được cùng đứa bạn thân nhong nhong trên khắp phố. (5) Hạnh phúc là ngồi co ro hàng giờ trong quán cà phê, nhấm nháp li ca-cao nóng và bàn chuyện chiến sự… thế giới cùng anh em chiến hữu…”.
(6) Bất chợt giật mình, hạnh phúc đơn giản vậy sao? (7) Ừ nhỉ! (8) Dường như lâu nay chúng ta chỉ quen với việc than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc. (9) Hãy một lần thử nghĩ xem: Khi chúng ta than phiền
Vì bố mẹ quá quan tâm đến chuyện của mình thì ngoài kia biết bao nhiêu người thèm hơi ấm của mẹ, thèm tiếng cười của bố, thèm được về nhà để được mắng; khi chúng ta cảm thấy thiệt thòi khi không được ngồi xe hơi chỉ
Vì phải chạy xe máy giữa trời nắng thì ngoài kia biết bao nhiêu bạn của chúng ta mồ hôi nhễ nhại, gò mình đạp xe lên những con dốc vắng; khi chúng ta bất mãn với chuyện học hành quá căng thẳng thì ngoài kia biết bao người đang khao khát một lần được đến trường, một lần được cầm cây bút để viết lên những ước mơ; khi chúng ta…
(Dẫn theo Bài tập Ngữ văn 11, tập 2, NXB Giáo dục 2007)
Từ “hạnh phúc”(in đậm, gạch chân) trong đoạn trích gần nghĩa hơn cả với từ ngữ nào?
-
Vui sướng
-
Nao nức
-
Hí hửng
-
Háo hức
-
Vui sướng
-
Nao nức
-
Hí hửng
-
Háo hức
(1) Một lần tình cờ tôi đọc được bài viết “Hạnh phúc là gì?” trên blốc của một người bạn. (2) Bạn ấy viết rằng: “Hạnh phúc là được nằm trong chăn ấm xem ti vi cùng với gia đình. (3) Hạnh phúc là được trùm chăn kín và được mẹ pha cho cốc sữa nóng. (4) Hạnh phúc là được cùng đứa bạn thân nhong nhong trên khắp phố. (5) Hạnh phúc là ngồi co ro hàng giờ trong quán cà phê, nhấm nháp li ca-cao nóng và bàn chuyện chiến sự… thế giới cùng anh em chiến hữu…”.
(6) Bất chợt giật mình, hạnh phúc đơn giản vậy sao? (7) Ừ nhỉ! (8) Dường như lâu nay chúng ta chỉ quen với việc than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc. (9) Hãy một lần thử nghĩ xem: Khi chúng ta than phiền
Vì bố mẹ quá quan tâm đến chuyện của mình thì ngoài kia biết bao nhiêu người thèm hơi ấm của mẹ, thèm tiếng cười của bố, thèm được về nhà để được mắng; khi chúng ta cảm thấy thiệt thòi khi không được ngồi xe hơi chỉ
Vì phải chạy xe máy giữa trời nắng thì ngoài kia biết bao nhiêu bạn của chúng ta mồ hôi nhễ nhại, gò mình đạp xe lên những con dốc vắng; khi chúng ta bất mãn với chuyện học hành quá căng thẳng thì ngoài kia biết bao người đang khao khát một lần được đến trường, một lần được cầm cây bút để viết lên những ước mơ; khi chúng ta…
(Dẫn theo Bài tập Ngữ văn 11, tập 2, NXB Giáo dục 2007)
Tại sao tác giả lại “Bất chợt giật mình, hạnh phúc đơn giản vậy sao?”?
-
Vì mọi người thường nghĩ hạnh phúc là cái cao xa, to lớn nhưng nó lại rất giản dị, gần gũi với chúng ta.
-
Vì hạnh phúc rất giản dị, gần gũi với chúng ta đồng thời là cái cao xa, to lớn mà con người không thể với tới được.
-
Vì hạnh phúc là cái cao xa, to lớn mà con người không thể với tới được.
-
Vì hạnh phúc rất phức tạp, không hề đơn giản
-
Vì mọi người thường nghĩ hạnh phúc là cái cao xa, to lớn nhưng nó lại rất giản dị, gần gũi với chúng ta.
-
Vì hạnh phúc rất giản dị, gần gũi với chúng ta đồng thời là cái cao xa, to lớn mà con người không thể với tới được.
-
Vì hạnh phúc là cái cao xa, to lớn mà con người không thể với tới được.
-
Vì hạnh phúc rất phức tạp, không hề đơn giản
(1) Một lần tình cờ tôi đọc được bài viết “Hạnh phúc là gì?” trên blốc của một người bạn. (2) Bạn ấy viết rằng: “Hạnh phúc là được nằm trong chăn ấm xem ti vi cùng với gia đình. (3) Hạnh phúc là được trùm chăn kín và được mẹ pha cho cốc sữa nóng. (4) Hạnh phúc là được cùng đứa bạn thân nhong nhong trên khắp phố. (5) Hạnh phúc là ngồi co ro hàng giờ trong quán cà phê, nhấm nháp li ca-cao nóng và bàn chuyện chiến sự… thế giới cùng anh em chiến hữu…”.
(6) Bất chợt giật mình, hạnh phúc đơn giản vậy sao? (7) Ừ nhỉ! (8) Dường như lâu nay chúng ta chỉ quen với việc than phiền mình bất hạnh chứ ít khi biết được rằng mình đang hạnh phúc. (9) Hãy một lần thử nghĩ xem: Khi chúng ta than phiền
Vì bố mẹ quá quan tâm đến chuyện của mình thì ngoài kia biết bao nhiêu người thèm hơi ấm của mẹ, thèm tiếng cười của bố, thèm được về nhà để được mắng; khi chúng ta cảm thấy thiệt thòi khi không được ngồi xe hơi chỉ
Vì phải chạy xe máy giữa trời nắng thì ngoài kia biết bao nhiêu bạn của chúng ta mồ hôi nhễ nhại, gò mình đạp xe lên những con dốc vắng; khi chúng ta bất mãn với chuyện học hành quá căng thẳng thì ngoài kia biết bao người đang khao khát một lần được đến trường, một lần được cầm cây bút để viết lên những ước mơ; khi chúng ta…
(Dẫn theo Bài tập Ngữ văn 11, tập 2, NXB Giáo dục 2007)
Chỉ ra biện pháp tu từ được sử dụng trong câu (9).
-
liệt kê, điệp ngữ, tương phản-đối lập.
-
liệt kê, tương phản- đối lập, so sánh
-
điệp ngữ, so sánh, liệt kê
-
điệp ngữ, tương phản- đối lập
-
liệt kê, điệp ngữ, tương phản-đối lập.
-
liệt kê, tương phản- đối lập, so sánh
-
điệp ngữ, so sánh, liệt kê
-
điệp ngữ, tương phản- đối lập
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Sinh vật trong tự nhiên rất phong phú và đa dạng, bao gồm những nhóm lớn sau: Vi khuẩn, Nấm, Thực vật và Động vật,… Chúng sống ở nhiều môi trường khác nhau, có quan hệ gần gũi với nhau và với con người”.
-
Động vật
-
gần gũi
-
phong phú
-
môi trường
-
Động vật
-
gần gũi
-
phong phú
-
môi trường
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Nghệ sĩ là người biết khai thác những ấn tượng riêng chủ quan của mình, tìm thấy những ấn tượng đó có giá trị khái quát và biết làm cho những ấn tượng đó có những hình thức riêng.
-
khai thác
-
khái quát
-
hình thức
-
chủ quan
-
khai thác
-
khái quát
-
hình thức
-
chủ quan
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Văn học Việt Nam, cả văn học dân gian và văn học viết, là sản phẩm tinh thần quý báu của dân tộc, phản ánh tâm hồn và tính cách Việt Nam với những nét bền vững đã thành truyền thống và có sự vận động trong trường ca lịch sử.
-
trường ca
-
phản ánh
-
truyền thống
-
sự vận động
-
trường ca
-
phản ánh
-
truyền thống
-
sự vận động
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Sài Gòn là thành phố trẻ trung, năng động, có nét hấp dẫn riêng về thiên nhiên và khí hậu. Người Sài Gòn có phong độ cởi mở, bộc trực, chân tình và trọng đạo nghĩa.
-
phong độ
-
năng động
-
trọng đạo nghĩa
-
hấp dẫn
-
phong độ
-
năng động
-
trọng đạo nghĩa
-
hấp dẫn
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Thơ hiện đại không chỉ đem lại những cái mới về nội dung tư tưởng, cảm xúc mà còn đổi mới về cách thức biểu cảm, về sáng tạo hình ảnh, cấu trúc câu thơ, ngôn ngữ thơ.
-
cách thức
-
tư tưởng
-
cấu trúc
-
sáng tạo
-
cách thức
-
tư tưởng
-
cấu trúc
-
sáng tạo
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
-
hạnh phúc
-
háo hức
-
náo nức
-
nô nức
-
hạnh phúc
-
háo hức
-
náo nức
-
nô nức
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
-
mưa
-
đạo đức
-
kinh nghiệm
-
cách mạng
-
mưa
-
đạo đức
-
kinh nghiệm
-
cách mạng
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
-
tham lam
-
tham khảo
-
tham quan
-
tham gia
-
tham lam
-
tham khảo
-
tham quan
-
tham gia
Đáp án KHÔNG phải đặc điểm ngôn ngữ của văn học Việt Nam giai đoạn từ đầu thế kí XX đến cách mạng tháng Tám năm 1945?
-
Lối diễn đạt công thức, ước lệ, tượng trưng, điển cố, quy phạm nghiêm ngặt của văn học trung đại vẫn được sử dụng và tuân thủ chặt chẽ
-
Ngôn ngữ gần gũi, hiện đại
-
Dần thoát li chữ Hán, chữ Nôm
-
Phát triển ngôn ngữ Tiếng Việt phong phú
-
Lối diễn đạt công thức, ước lệ, tượng trưng, điển cố, quy phạm nghiêm ngặt của văn học trung đại vẫn được sử dụng và tuân thủ chặt chẽ
-
Ngôn ngữ gần gũi, hiện đại
-
Dần thoát li chữ Hán, chữ Nôm
-
Phát triển ngôn ngữ Tiếng Việt phong phú
Đặc điểm nào KHÔNG phải là đặc điểm cơ bản của nền văn học Việt Nam từ năm 1945 đến năm 1975?
-
Nền văn học đổi mới theo hướng hiện đại hóa.
-
Nền văn học chủ yếu vận động theo hướng cách mạng hoá, gắn bó sâu sắc với vận mệnh chung của đất nước.
-
Nền văn học chủ yếu mang khuynh hướng sử thi và cảm hứng lãng mạn.
-
Nền văn học hướng về đại chúng.
-
Nền văn học đổi mới theo hướng hiện đại hóa.
-
Nền văn học chủ yếu vận động theo hướng cách mạng hoá, gắn bó sâu sắc với vận mệnh chung của đất nước.
-
Nền văn học chủ yếu mang khuynh hướng sử thi và cảm hứng lãng mạn.
-
Nền văn học hướng về đại chúng.
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tình huống là một ______ của sự sống, là một sự kiện diễn ra có phần bất ngờ nhưng cái quan trọng là sẽ chi phối nhiều điều trong cuộc sống con người.
-
lát cắt
-
dấu ấn
-
phương thức
-
mảnh ghép
-
lát cắt
-
dấu ấn
-
phương thức
-
mảnh ghép
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
_______là người có tấm lòng thật đôn hậu, chan chứa yêu thương. Ông gắn bó sâu nặng, giàu ân tình với quê hương và những người nghèo khổ bị áp bức, khinh miệt trong xã hội cũ.
-
Nam Cao
-
Vũ Trọng Phụng
-
Nguyễn Minh Châu
-
Thạch Lam
Giải chi tiết:
Nam Cao là người có tấm lòng thật đôn hậu, chan chứa yêu thương. Ông gắn bó sâu nặng, giàu ân tình với quê hương và những người nghèo khổ bị áp bức, khinh miệt trong xã hội cũ.
-
Nam Cao
-
Vũ Trọng Phụng
-
Nguyễn Minh Châu
-
Thạch Lam
Giải chi tiết:
Nam Cao là người có tấm lòng thật đôn hậu, chan chứa yêu thương. Ông gắn bó sâu nặng, giàu ân tình với quê hương và những người nghèo khổ bị áp bức, khinh miệt trong xã hội cũ.
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
_______là dùng lí lẽ và chứng cứ để gạt bỏ những quan điểm, ý kiến sai lệch hoạc thiếu chính xác,…từ đó, nêu ý kiến đúng của mình để thuyết phục người nghe (người đọc).
-
Bác bỏ
-
Giải thích
-
Nghị luận
-
Chứng minh
-
Bác bỏ
-
Giải thích
-
Nghị luận
-
Chứng minh
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
______ là một kiệt tác trong văn xuôi Việt Nam hiện đại, một truyện ngắn có giá trị hiện thực và nhân đạo sâu sắc, mới mẻ, chứng tỏ trình độ nghệ thuật bậc thầy của một nhà văn lớn.
-
Chí Phèo
-
Số đỏ
-
Hai đứa trẻ
-
Vợ nhặt
-
Chí Phèo
-
Số đỏ
-
Hai đứa trẻ
-
Vợ nhặt
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Ngôn ngữ báo chí là ngôn ngữ thông tin thời sự cập nhật, ______ những tin tức nóng hổi hằng ngày trên mọi lĩnh vực hoạt động của xã hội.
-
truyền bá
-
truyền tụng
-
truyền hình
-
lan truyền
Điền từ.
Giải chi tiết:
Ngôn ngữ báo chí là ngôn ngữ thông tin thời sự cập nhật, truyền bá những tin tức nóng hổi hằng ngày trên mọi lĩnh vực hoạt động của xã hội.
-
truyền bá
-
truyền tụng
-
truyền hình
-
lan truyền
Điền từ.
Giải chi tiết:
Ngôn ngữ báo chí là ngôn ngữ thông tin thời sự cập nhật, truyền bá những tin tức nóng hổi hằng ngày trên mọi lĩnh vực hoạt động của xã hội.
“Áo chàm đưa buổi phân li
Cầm tay nhau biết nói gì hôm nay…”
(Trích đoạn trích Việt Bắc, Tố Hữu, SGK Ngữ văn lớp 12, tập 1)
Hình ảnh “Cầm tay nhau biết nói gì hôm nay” diễn tả những cung bậc cảm xúc nào?
-
Nỗi nhớ nhung, lưu luyến, bịn rịn giữa kẻ ở và người đi
-
Diễn tả tình cảm quân dân gắn bó, tha thiết
-
Diễn tả những tình cảm cách mạng lớn lao
-
Diễn tả tình cảm đồng cam cộng khổ giữa kẻ ở và người đi
-
Nỗi nhớ nhung, lưu luyến, bịn rịn giữa kẻ ở và người đi
-
Diễn tả tình cảm quân dân gắn bó, tha thiết
-
Diễn tả những tình cảm cách mạng lớn lao
-
Diễn tả tình cảm đồng cam cộng khổ giữa kẻ ở và người đi
“Tỉnh dậy hắn thấy già mà vẫn còn cô độc. Buồn thay cho đời! Có lý nào như thế được? Hắn đã già rồi hay sao? Ngoài bốn mươi tuổi đầu… Dẫu sao, đó không phải tuổi mà người ta mới bắt đầu sửa soạn. Hắn đã tới cái dốc bên kia của đời. Ở những người như hắn, chịu đựng biết bao nhiêu là chất độc, đầy đọa cực nhọc mà chưa bao giờ ốm, một trận ốm có thể gọi là dấu hiệu báo rằng cơ thể đã hư hỏng nhiều. Nó là một cơn mưa gió cuối thu cho biết trời gió rét, nay mùa đông đã đến. Chí Phèo hình như đã trông thấy trước tuổi già của hắn, đói rét và ốm đau, và cô độc, cái này còn đáng sợ hơn đói rét và ốm đau.”
(Trích đoạn trích Chí Phèo, Nam Cao, SGK Ngữ văn lớp 11, tập 1)
Xác định biện pháp tu từ được sử dụng trong câu: Hắn đã tới cái dốc bên kia của đời.
-
Ẩn dụ
-
So sánh
-
Nhân hóa
-
Hoán dụ
-
Ẩn dụ
-
So sánh
-
Nhân hóa
-
Hoán dụ
Đẩu gật đầu. Anh đứng dậy. Tự nhiên anh rời chiếc bàn đến đứng vịn vào lưng ghế người đàn bà ngồi giọng trở
Nên đầy giận dữ, khác hẳn với giọng một vị chánh án:
– Ba ngày một trận nhẹ, năm ngày một trận nặng. Cả nước không có một người chồng nào như hắn. Tôi chưa hỏi tội của hắn mà tôi chỉ muốn bảo ngay với chị: chị không sống nổi với cái lão đàn ông vũ phu ấy đâu. Chị nghĩ thế nào?
Người đàn bà hướng về phía Đẩu, tự nhiên chắp tay vái lia lịa:
– Con lạy quý tòa…
– Sao, sao?
– Quý tòa bắt tội con cũng được, phạt tù con cũng được, đừng bắt con bỏ nó…
(Trích Chiếc thuyền ngoài xa – Nguyễn Minh Châu, Ngữ văn 12, Tập hai, NXB Giáo dục)
Tại sao người đàn bà hàng chài lại van xin quý tòa đừng bắt phải bỏ người chồng vũ phu của mình?
-
Vì chị là một người mẹ thương con và là một người vợ hiểu chồng
-
Vì chị hiểu là người chồng khổ quá
Nên mới trút nỗi hận vào người vợ
-
Vì người chồng là người đã cưu mang, cứu giúp chị
Nên chị phải đền ơn
-
Vì chị không thể một mình nuôi nấng những đứa con
-
Vì chị là một người mẹ thương con và là một người vợ hiểu chồng
-
Vì chị hiểu là người chồng khổ quá
Nên mới trút nỗi hận vào người vợ -
Vì người chồng là người đã cưu mang, cứu giúp chị
Nên chị phải đền ơn -
Vì chị không thể một mình nuôi nấng những đứa con
Đất Nước là nơi ta hò hẹn
Đất Nước là nơi em đánh rơi chiếc khăn trong nỗi nhớ thầm
Đất là nơi “con chim phượng hoàng bay về hòn núi bạc”
Nước là nơi “con cá ngư ông móng nước biển khơi”
Thời gian đằng đẵng
Không gian mệnh mông
Đất Nước là nơi dân mình đoàn tụ
Đất là nơi Chim về
Nước là nơi Rồng ở
Lạc Long Quân và Âu Cơ
Đẻ ra đồng bào ta trong bọc trứng
(Trích Đất nước – Nguyễn Khoa Điểm, Ngữ văn 12, Tập một, NXB Giáo dục)
Sử dụng chất liệu văn hóa dân gian trong đoạn thơ “Đất Nước”, Nguyễn Khoa Điểm nhằm thể hiện:
-
Niềm tự hào về truyền thống lịch sử.
-
Tư tưởng Đất Nước của nhân dân.
-
Hình tượng một Đất Nước bình dị.
-
Lí giải sự hình thành Đất Nước.
-
Niềm tự hào về truyền thống lịch sử.
-
Tư tưởng Đất Nước của nhân dân.
-
Hình tượng một Đất Nước bình dị.
-
Lí giải sự hình thành Đất Nước.
Bèo dạt về đâu, hàng nối hàng;
Mênh mông không một chuyến đò ngang.
Không cầu gợi chút niềm thân mật,
Lặng lẽ bờ xanh tiếp bãi vàng.
(Tràng Giang– Huy Cận, Ngữ văn 11, Tập một, NXB Giáo dục)
Cái cảm giác trống trải, xa vắng của không gian “tràng giang” trong khổ thơ thứ ba, chủ yếu được tô đậm bởi yếu tố nghệ thuật nào?
-
Điệp từ và từ phủ định
-
Cảnh ngụ tình
-
Ẩn dụ
-
Âm hưởng, nhạc điệu
-
Điệp từ và từ phủ định
-
Cảnh ngụ tình
-
Ẩn dụ
-
Âm hưởng, nhạc điệu
…Còn xa lắm mới đến cái thác dưới. Nhưng đã thấy tiếng nước réo gần mãi lại, réo to mãi lên. Tiếng nước thác nghe như là oán trách gì, rồi lại như là van xin, rồi lại như là khiêu khích, giọng gằn mà chế nhạo. Thế rồi nó rống lên như tiếng một ngàn con trâu mộng đang lồng lộn giữa rừng vầu, rừng tre nứa nổ lửa, đang phá tuông rừng lửa, rừng lửa cùng gầm thét với đàn trâu da cháy bùng bùng. Tới cái thác rồi. Ngoặt khúc sông lượn, thấy sóng bọt đã trắng xóa cả chân trời đá. Đá ở đây từ ngàn năm vẫn mai phục hết trong lòng sông, hình như mỗi lần có chiếc thuyền nào xuất hiện ở quãng ầm ầm mà quạnh hiu này, mỗi lần có chiếc nào nhô vào đường ngoặt sông là một số hòn bèn nhổm cả dậy để vồ lấy thuyền. Mặt hòn đá nào trông cũng ngỗ ngược, hòn nào cũng nhăn nhúm méo mó hơn cả cái mặt nước chỗ này.
(Người lái đò sông Đà – Nguyễn Tuân, Ngữ văn 12, Tập một, NXB Giáo dục)
Nội dung của đoạn trích là gì?
-
Tả về thác nước và đá ở sông Đà ( hay còn gọi là thạch thuỷ trận)
-
Sự dữ dội, mãnh liệt của dòng sông hung bạo
-
Cảnh ven sông Đà ở hạ nguồn thơ mộng, lặng tờ, dạt dào sức sống
-
Sông Đà thơ mộng, trữ tình, hoang sơ
-
Tả về thác nước và đá ở sông Đà ( hay còn gọi là thạch thuỷ trận)
-
Sự dữ dội, mãnh liệt của dòng sông hung bạo
-
Cảnh ven sông Đà ở hạ nguồn thơ mộng, lặng tờ, dạt dào sức sống
-
Sông Đà thơ mộng, trữ tình, hoang sơ
Dẫu xuôi về phương Bắc
Dẫu ngược về phương Nam
Nơi nào em cũng nghĩ
Hướng về anh – một phương
(Sóng – Xuân Quỳnh, Ngữ văn 12, Tập một, NXB Giáo dục)
Khổ thơ nói lên được phẩm chất nào trong tình yêu của người phụ nữ?
-
Thủy chung
-
Đôn hậu
-
Say đắm
-
Nhớ nhung
-
Thủy chung
-
Đôn hậu
-
Say đắm
-
Nhớ nhung
Phải nhiều thế kỉ qua đi, người tình mong đợi mới đến đánh thức người gái đẹp nằm ngủ mơ màng giữa cánh đồng Châu Hóa đầy hoa dại. Nhưng ngay từ đầu vừa ra khỏi vùng núi, sông Hương đã chuyển dòng một cách liên tục, vòng giữa khúc quanh đột ngột, uốn mình theo những đường cong thật mềm, như một cuộc tìm kiếm có ý thức để đi tới nơi gặp thành phố tương lai của nó. Từ ngã ba Tuần, sông Hương theo hướng nam bắc qua điện Hòn Chén; vấp Ngọc Trản, nó chuyển hướng sang tây bắc, vòng qua thềm đất bãi Nguyệt Biều, Lương Quán rồi đột ngột vẽ một hình cung thật tròn về phía đông bắc, ôm lấy chân đồi Thiên Mụ, xuôi dần về Huế. Từ Tuần về đây, sông Hương vẫn đi trong dư vang của Trường Sơn, vượt qua một lòng vực sâu dưới chân núi Ngọc Trản để sắc nước trở
Nên xanh thẳm, và từ đó nó trôi đi giữa hai dãy đồi sừng sững như thành quách, với những điểm cao đột ngột như Vọng Cảnh, Tam Thai, Lựu Bảo mà từ đó, người ta luôn luôn nhìn thấy dòng sông mềm như tấm lụa, với những chiếc thuyền xuôi ngược chỉ bé vừa bằng con thoi. Những ngọn đồi này tạo
Nên những mảng phản quang nhiều màu sắc trên nền trời tây nam thành phố, “sớm xanh, trưa vàng, chiều tím” như người Huế thường miêu tả. Giữa đám quần sơn lô xô ấy, là giấc ngủ nghìn năm của những vua chúa được phong kín trong lòng những rừng thông u tịch và niềm kiêu hãnh âm u của những lăng tẩm đồ sộ tỏa lan khắp cả một vùng thượng lưu “Bốn bề núi phủ mây phong – Mảnh trăng thiên cổ bóng tùng Vạn Niên”. Đó là vẻ đẹp trầm mặc nhất của sông Hương, như triết lí, như cổ thi, kéo dài mãi đến lúc mặt nước phẳng lặng của nó gặp tiếng chuông chùa Thiên Mụ ngân nga tận bờ bên kia, giữa những xóm làng trung du bát ngát tiếng gà…
(Trích Ai đã đặt tên cho dòng sông – Hoàng Phủ Ngọc Tường, Ngữ văn 12, Tập một, NXB Giáo dục)
Vẻ đẹp của dòng sông Hương được thể hiện trong đoạn trích trên là gì?
-
Sông Hương mang vẻ đẹp vừa mạnh mẽ, vừa dịu dàng, vừa cổ kính, trầm mặc đậm chất Huế.
-
Sông Hương đẹp như điệu slow chậm rãi, sâu lắng, trữ tình và với cái nhìn đắm say của một trái tim đa tình.
-
Sông Hương mang vẻ đẹp kín đáo của tâm hồn sâu thẳm .
-
Sông Hương bí ẩn mà hùng vĩ, mãnh liệt .
-
Sông Hương mang vẻ đẹp vừa mạnh mẽ, vừa dịu dàng, vừa cổ kính, trầm mặc đậm chất Huế.
-
Sông Hương đẹp như điệu slow chậm rãi, sâu lắng, trữ tình và với cái nhìn đắm say của một trái tim đa tình.
-
Sông Hương mang vẻ đẹp kín đáo của tâm hồn sâu thẳm .
-
Sông Hương bí ẩn mà hùng vĩ, mãnh liệt .
Bà lão cúi đầu nín lặng. Bà lão hiểu rồi. Lòng người mẹ nghèo khổ ấy còn hiểu ra biết bao nhiêu cơ sự, vừa ai oán vừa xót thương cho số kiếp đứa con mình. Chao ôi, người ta dựng vợ gả chồng cho con là lúc trong nhà ăn
Nên làm nổi, những mong sinh con đẻ cái mở mặt sau này. Còn mình thì… Trong kẽ mắt kèm nhèm của bà rủ xuống hai dòng nước mắt… Biết rằng chúng nó có nuôi nổi nhau sống qua được cơn đói khát này không?
(Trích Vợ nhặt – Kim Lân, Ngữ văn 12, Tập hai, NXB Giáo dục)
Xác định thành ngữ dân gian được sử dụng trong đoạn văn
-
dựng vợ gả chồng, ăn
Nên làm nổi, sinh con đẻ cái.
-
ăn nên làm nổi, sinh con đẻ cái, cúi đầu nín lặng.
-
dựng vợ gả chồng, cúi đầu nín lặng, ăn nên làm nổi.
-
cúi đầu nín lặng, dựng vợ gả chồng, sinh con đẻ cái.
-
dựng vợ gả chồng, ăn
Nên làm nổi, sinh con đẻ cái. -
ăn nên làm nổi, sinh con đẻ cái, cúi đầu nín lặng.
-
dựng vợ gả chồng, cúi đầu nín lặng, ăn nên làm nổi.
-
cúi đầu nín lặng, dựng vợ gả chồng, sinh con đẻ cái.
Một ngón tay Tnú bốc cháy. Hai ngón, ba ngón. Không có gì đượm bằng nhựa xà nu. Lửa bắt rất nhanh. Mười ngón tay đã thành mười ngọn đuốc.
Tnú nhắm mắt lại, rồi mở mắt ra, nhìn trừng trừng.
Trời ơi! Cha mẹ ơi! Anh không cảm thấy lửa cháy ở mười đầu ngón tay nữa. Anh nghe lửa cháy trong lồng ngực, cháy ở bụng. Máu anh mặn chát ở đầu lưỡi. Răng anh đã cắn nát môi anh rồi. Anh không kêu rên. Anh Quyết nói: “Người Cộng sản không thèm kêu van…” Tnú không thèm, không thèm kêu van. Nhưng trời ơi! Cháy! Không, Tnú sẽ không kêu! Không!
(Trích Rừng Xà Nu – Nguyễn Trung Thành, Ngữ văn 11, Tập hai, NXB Giáo dục)
Xác định phương thức biểu đạt của đoạn văn trên?
-
Phương thức tự sự
-
Phương thức miêu tả
-
Phương thức biểu cảm
-
Phương thức nghị luận
Căn cứ vào các phương thức biểu đạt đã học.
Giải chi tiết:
Phương thức tự sự Vì đây là lời kể chuyện của nhân vật cụ Mết trong đêm Tnú về thăm làng Xô Man sau ba năm đi lực lượng.
-
Phương thức tự sự
-
Phương thức miêu tả
-
Phương thức biểu cảm
-
Phương thức nghị luận
Căn cứ vào các phương thức biểu đạt đã học.
Giải chi tiết:
Phương thức tự sự Vì đây là lời kể chuyện của nhân vật cụ Mết trong đêm Tnú về thăm làng Xô Man sau ba năm đi lực lượng.
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Từ ấy trong tôi bừng nắng hạ
Mặt trời chân lí chói qua tim
Hồn tôi là một vườn hoa lá
Rất đậm hương và rộn tiếng chim…
(Từ ấy – Tố Hữu, Ngữ văn 11, tập hai, NXB Giáo dục)
Chỉ ra biện pháp nghệ thuật được sử dụng trong đoạn thơ trên.
-
So sánh, ẩn dụ
-
So sánh, điệp ngữ
-
Ẩn dụ, nhân hóa
-
So sánh, nhân hóa
-
So sánh, ẩn dụ
-
So sánh, điệp ngữ
-
Ẩn dụ, nhân hóa
-
So sánh, nhân hóa
“…Rải rác biên cương mồ viễn xứ
Chiến trường đi chẳng tiếc đời xanh
Áo bào thay chiếu anh về đất
Sông Mã gầm lên khúc độc hành…”
( trích Tây Tiến – Quang Dũng, Ngữ văn lớp 12, tập một, NXB Giáo dục)
Nêu ý nghĩa tu từ của từ “anh về đất” trong đoạn thơ.
-
Biện pháp nói giảm, nói tránh để chỉ cái chết của người lính
-
Vẻ đẹp tâm hồn của người lính Tây Tiến
-
Nhấn mạnh đến sức mạnh khí phách của những người lính.
-
Khí thế hào hùng và một thế giới tâm hồn hết sức lãng mạn
-
Biện pháp nói giảm, nói tránh để chỉ cái chết của người lính
-
Vẻ đẹp tâm hồn của người lính Tây Tiến
-
Nhấn mạnh đến sức mạnh khí phách của những người lính.
-
Khí thế hào hùng và một thế giới tâm hồn hết sức lãng mạn
Quyện điểu quy lâm tầm túc thụ
Cô vân mạn mạn độ thiên không
Sơn thôn thiếu nữ ma bao túc
Bao túc ma hoàn, lô dĩ hồng
(Chiều tối – Hồ Chí Minh, Ngữ văn 11, Tập một, NXB Giáo dục)
Hai câu đầu bài thơ “Chiều tối” gợi lên trong lòng người đọc cảm giác gì rõ nhất ?
-
Sự mệt mỏi, cô quạnh
-
Sự cô đơn, trống vắng
-
Sự buồn chán, hiu hắt
-
Sự bâng khuâng, buồn bã
-
Sự mệt mỏi, cô quạnh
-
Sự cô đơn, trống vắng
-
Sự buồn chán, hiu hắt
-
Sự bâng khuâng, buồn bã
Thôn Đoài ngồi nhớ thôn Đông
Một người chín nhớ mười mong một người.
Gió mưa là bệnh của giời,
Tương tư là bệnh của tôi yêu nàng
(Nguyễn Bính – Tương tư, Ngữ văn 11, Tập hai, NXB Giáo dục)
Đoạn thơ thể hiện tâm tư,tình cảm gì của nhân vật trữ tình?
-
Tâm trạng tương tư – nhớ nhung của nhân vật trữ tình.
-
Tâm trạng cô đơn, xót xa của nhân vật trữ tình.
-
Tâm trạng buồn, cô đơn của nhân vật trữ tình.
-
Tâm trạng da diết của nhân vật trữ tình.
-
Tâm trạng tương tư – nhớ nhung của nhân vật trữ tình.
-
Tâm trạng cô đơn, xót xa của nhân vật trữ tình.
-
Tâm trạng buồn, cô đơn của nhân vật trữ tình.
-
Tâm trạng da diết của nhân vật trữ tình.
“Tiếng trống thu không trên cái chòi của huyện nhỏ; từng tiếng một vang ra để gọi buổi chiều. Phương tây đỏ rực như lửa cháy và những đám mây ánh hồng như hòn than sắp tàn. Dãy tre làng trước mặt đen lại và cắt hình rõ rệt trên nền trời. Chiều, chiều rồi. Một chiều êm ả như ru, văng vẳng tiếng ếch nhái kêu ran ngoài đồng ruộng theo gió nhẹ đưa vào. Trong cửa hàng hơi tối muỗi đã bắt đầu vo ve. Liên ngồi yên lặng bên mấy quả thuốc sơn đen ; đôi mắt chị bóng tối ngập đầy dần và cái buồn của buổi chiều quê thấm thía vào tâm hồn ngây thơ của chị ; Liên không hiểu sao, nhưng chị thấy lòng buồn man mác trước cái giờ khắc của ngày tàn.”
(Trích Hai đứa trẻ – Thạch Lam, SGK Ngữ văn 11 tập 1, NXBGD)
Nội dung chính của đoạn trích là gì?
-
Bức tranh phố huyện lúc chiều tàn
-
Bức tranh phố huyện lúc về đêm khuya
-
Bức tranh phố huyện lúc chuyến tàu đi qua
-
Bức tranh phố huyện
-
Bức tranh phố huyện lúc chiều tàn
-
Bức tranh phố huyện lúc về đêm khuya
-
Bức tranh phố huyện lúc chuyến tàu đi qua
-
Bức tranh phố huyện
Sự kiện mở đầu cho cuộc cách mạng tháng Hai năm 1917 ở Nga là
-
cuộc biểu tình của 9 vạn nữ công nhân ở Thủ đô Pê-tơ-rô-grat.
-
cuộc tấn công của các đội Cận vệ đỏ để chiếm các vị trí then chốt.
-
quân khởi nghĩa tân công vào cung điện Mùa Đông.
-
Nga hoàng Nicôlai II tuyên bố thoái vị.
-
cuộc biểu tình của 9 vạn nữ công nhân ở Thủ đô Pê-tơ-rô-grat.
-
cuộc tấn công của các đội Cận vệ đỏ để chiếm các vị trí then chốt.
-
quân khởi nghĩa tân công vào cung điện Mùa Đông.
-
Nga hoàng Nicôlai II tuyên bố thoái vị.
Với tác động từ cuộc khai thác thuộc địa lần thứ hai của thực dân Pháp (1919 – 1929), nền kinh tế Việt Nam
-
phổ biến vẫn trong tình trạng nghèo nàn, lạc hậu.
-
có điều kiện phát triển độc lập với kinh tế Pháp.
-
. có sự chuyển biến rất nhanh và mạnh về cơ cấu.
-
có đủ khả năng cạnh tranh với nền kinh tế Pháp.
-
phổ biến vẫn trong tình trạng nghèo nàn, lạc hậu.
-
có điều kiện phát triển độc lập với kinh tế Pháp.
-
. có sự chuyển biến rất nhanh và mạnh về cơ cấu.
-
có đủ khả năng cạnh tranh với nền kinh tế Pháp.
Hội nghị lần thứ nhất Ban Chấp hành Trung ương lâm thời Đảng Cộng sảnViệt Nam (tháng10-1930) quyết định đổi tên Đảng thành
-
Đảng Cộng sản Đông Dương.
-
Đảng Lao động Việt Nam.
-
An Nam Cộng sản đảng.
-
Đông Dương Cộng sản liên đoàn.
-
Đảng Cộng sản Đông Dương.
-
Đảng Lao động Việt Nam.
-
An Nam Cộng sản đảng.
-
Đông Dương Cộng sản liên đoàn.
Kế hoạch Đờ Lát đơ Tatxinhi ra đời là kết quả của
-
sự cấu kết giữa Pháp và Mĩ trong việc đẩy mạnh cuộc chiến ở Đông Dương.
-
sự can thiệp sâu nhất của Mĩ vào chiến tranh xâm lược Đông Dương.
-
sự “dính líu trực tiếp” của Mĩ vào chiến tranh xâm lược Đông Dương.
-
sự viện trợ cao nhất của Mĩ và nỗ lực lớn nhất của Pháp trong chiến tranh.
-
sự cấu kết giữa Pháp và Mĩ trong việc đẩy mạnh cuộc chiến ở Đông Dương.
-
sự can thiệp sâu nhất của Mĩ vào chiến tranh xâm lược Đông Dương.
-
sự “dính líu trực tiếp” của Mĩ vào chiến tranh xâm lược Đông Dương.
-
sự viện trợ cao nhất của Mĩ và nỗ lực lớn nhất của Pháp trong chiến tranh.
Cơ quan ngôn luận của Hội Việt Nam Cách mạng Thanh niên là:
-
Báo Thanh niên.
-
Tác phẩm “Đường Cách mệnh”.
-
Bàn ăn chế độ tư bản Pháp.
-
Bảo Người Cũng khổ.
-
Báo Thanh niên.
-
Tác phẩm “Đường Cách mệnh”.
-
Bàn ăn chế độ tư bản Pháp.
-
Bảo Người Cũng khổ.
Kế hoạch Nava là sản phẩm của
-
sự kết hợp sức mạnh của Mĩ và thủ đoạn của thực dân Pháp.
-
sự nỗ lực cao nhất, cuối cùng của thực dân Pháp ở Đông Dương.
-
thủ đoạn mới của đế quốc Mĩ và sức mạnh của thực dân Pháp.
-
sự can thiệp sâu nhât của đế quốc Mĩ vào Đông Dương.
-
sự kết hợp sức mạnh của Mĩ và thủ đoạn của thực dân Pháp.
-
sự nỗ lực cao nhất, cuối cùng của thực dân Pháp ở Đông Dương.
-
thủ đoạn mới của đế quốc Mĩ và sức mạnh của thực dân Pháp.
-
sự can thiệp sâu nhât của đế quốc Mĩ vào Đông Dương.
Chiến dịch Biên giới thu – đông năm 1950 ở Việt Nam được mở trong bối cảnh lịch sử nào sau đây?
-
Mĩ đang từng bước can thiệp vào chiến tranh ở Việt Nam.
-
Thực dân Pháp mở cuộc tấn công quy mô lớn lên Việt Bắc.
-
Thực dân Pháp muốn chấm dứt chiến tranh trong danh dự.
-
Mĩ đang hỗ trợ thực dân Pháp triển khai kế hoạch Nava.
-
Mĩ đang từng bước can thiệp vào chiến tranh ở Việt Nam.
-
Thực dân Pháp mở cuộc tấn công quy mô lớn lên Việt Bắc.
-
Thực dân Pháp muốn chấm dứt chiến tranh trong danh dự.
-
Mĩ đang hỗ trợ thực dân Pháp triển khai kế hoạch Nava.
“Ba mươi năm ấy chân không mỏi/ Mà đến bây giờ mới tới nơi” (Tố Hữu), là hai câu thơ nói về sự kiện nào?
-
Nguyễn Ái Quốc về nước.
-
Nguyễn Ái Quốc sang Liên Xô.
-
Nguyễn Ái Quốc đến Trung Quốc.
-
Nguyễn Ái Quốc sang Xiêm.
-
Nguyễn Ái Quốc về nước.
-
Nguyễn Ái Quốc sang Liên Xô.
-
Nguyễn Ái Quốc đến Trung Quốc.
-
Nguyễn Ái Quốc sang Xiêm.
Sau đại thắng mùa Xuân 1975, Tổ quốc Việt Nam được thống nhất về mặt lãnh thổ, song ở mỗi miền vẫn tồn tại hình thức tổ chức nhà nước khác nhau. Thực tế đó trái với nguyện vọng, tình cảm thiêng liêng của nhân dân hai miền Bắc – Nam là sớm được sum họp trong một đại gia đình, mong muốn có một chính phủ thống nhất, một cơ quan đại diện quyền lực chung cho nhân dân cả nước.
Đáp lại nguyện vọng chính đáng của nhân dân cả nước, đồng thời cũng phù hợp với thực tế lịch sử dân tộc – “Nước Việt Nam là một, dân tộc Việt Nam là một” – Hội nghị lần thứ 24 Ban Chấp hành Trung ương Đảng (9 – 1975) đề ra nhiệm vụ hoàn thành thống nhất đất nước về mặt nhà nước.
Từ ngày 15 đến ngày 21 – 11 – 1975, Hội nghị Hiệp thương chính trị thống nhất đất nước được tổ chức tại Sài Gòn. Hai đoàn đại biểu đại diện cho hai miền tham dự. Hội nghị nhất trí hoàn toàn các vấn đề về chủ trương, biện pháp nhằm thống nhất đất nước về mặt nhà nước.
Ngày 25 – 4 – 1976, cuộc Tổng tuyển cử bầu Quốc hội chung được tiến hành trong cả nước. Hơn 23 triệu cử tri (chiếm 98,8% tổng số cử tri đi bỏ phiếu và bầu ra 492 đại biểu.
Từ ngày 24 – 6 đến ngày 3 – 7 – 1976, Quốc hội khoá VI nước Việt Nam thống nhất học kì đầu tiên tại Hà Nội.
Quốc hội thông qua chính sách đối nội và đối ngoại của Nhà nước Việt Nam thống nhất, quyết định tên nước là Cộng hoà xã hội chủ nghĩa Việt Nam (từ ngày 2 – 7 – 1976), quyết định Quốc huy mang dòng chữ Cộng hoà xã hội chủ nghĩa Việt Nam, Quốc kì là lá cờ đỏ sao vàng, Quốc ca là bài Tiến quân ca, thủ đô là Hà Nội, thành phố Sài Gòn – Gia Định được đổi tên là Thành phố Hồ Chí Minh.
Quốc hội bầu các cơ quan, chức vụ lãnh đạo cao nhất của nước Cộng hoà xã hội chủ nghĩa Việt Nam, bầu Ban dự thảo Hiến pháp.
(Nguồn: SGK Lịch sử 12, trang 201 – 202)
Sau đại thắng mùa Xuân 1975, nhiệm vụ cấp thiết hàng đầu của cả nước là
-
thống nhất đất nước về mặt nhà nước.
-
ổn định tình hình chính trị – xã hội ở miền Nam.
-
khắc phục hậu quả chiến tranh và phát triển kinh tế.
-
mở rộng quan hệ giao lưu với các nước.
-
thống nhất đất nước về mặt nhà nước.
-
ổn định tình hình chính trị – xã hội ở miền Nam.
-
khắc phục hậu quả chiến tranh và phát triển kinh tế.
-
mở rộng quan hệ giao lưu với các nước.
Sau đại thắng mùa Xuân 1975, Tổ quốc Việt Nam được thống nhất về mặt lãnh thổ, song ở mỗi miền vẫn tồn tại hình thức tổ chức nhà nước khác nhau. Thực tế đó trái với nguyện vọng, tình cảm thiêng liêng của nhân dân hai miền Bắc – Nam là sớm được sum họp trong một đại gia đình, mong muốn có một chính phủ thống nhất, một cơ quan đại diện quyền lực chung cho nhân dân cả nước.
Đáp lại nguyện vọng chính đáng của nhân dân cả nước, đồng thời cũng phù hợp với thực tế lịch sử dân tộc – “Nước Việt Nam là một, dân tộc Việt Nam là một” – Hội nghị lần thứ 24 Ban Chấp hành Trung ương Đảng (9 – 1975) đề ra nhiệm vụ hoàn thành thống nhất đất nước về mặt nhà nước.
Từ ngày 15 đến ngày 21 – 11 – 1975, Hội nghị Hiệp thương chính trị thống nhất đất nước được tổ chức tại Sài Gòn. Hai đoàn đại biểu đại diện cho hai miền tham dự. Hội nghị nhất trí hoàn toàn các vấn đề về chủ trương, biện pháp nhằm thống nhất đất nước về mặt nhà nước.
Ngày 25 – 4 – 1976, cuộc Tổng tuyển cử bầu Quốc hội chung được tiến hành trong cả nước. Hơn 23 triệu cử tri (chiếm 98,8% tổng số cử tri đi bỏ phiếu và bầu ra 492 đại biểu.
Từ ngày 24 – 6 đến ngày 3 – 7 – 1976, Quốc hội khoá VI nước Việt Nam thống nhất học kì đầu tiên tại Hà Nội.
Quốc hội thông qua chính sách đối nội và đối ngoại của Nhà nước Việt Nam thống nhất, quyết định tên nước là Cộng hoà xã hội chủ nghĩa Việt Nam (từ ngày 2 – 7 – 1976), quyết định Quốc huy mang dòng chữ Cộng hoà xã hội chủ nghĩa Việt Nam, Quốc kì là lá cờ đỏ sao vàng, Quốc ca là bài Tiến quân ca, thủ đô là Hà Nội, thành phố Sài Gòn – Gia Định được đổi tên là Thành phố Hồ Chí Minh.
Quốc hội bầu các cơ quan, chức vụ lãnh đạo cao nhất của nước Cộng hoà xã hội chủ nghĩa Việt Nam, bầu Ban dự thảo Hiến pháp.
(Nguồn: SGK Lịch sử 12, trang 201 – 202)
Sự kiện nào là quan trọng nhất trong quá trình thống nhất đất nước về mặt Nhà nước sau 1975?
-
Tổng tuyển cử bầu Quốc hội chung trong cả nước (25/4/1976).
-
Quốc hội khóa XI của nước Việt Nam thống nhất kỳ họp đầu tiên.
-
Đại hội thống nhất mặt trận Tổ quốc Việt Nam.
-
Hội nghị Hiệp thương của đại biểu hai miền Bắc Nam tại Sài Gòn (11/1975).
-
Tổng tuyển cử bầu Quốc hội chung trong cả nước (25/4/1976).
-
Quốc hội khóa XI của nước Việt Nam thống nhất kỳ họp đầu tiên.
-
Đại hội thống nhất mặt trận Tổ quốc Việt Nam.
-
Hội nghị Hiệp thương của đại biểu hai miền Bắc Nam tại Sài Gòn (11/1975).
Hạn chế lớn nhất trong phát triển công nghiệp Nhật Bản là
-
thiếu nguyên, nhiên liệu.
-
thị trường bị thu hẹp.
-
thiếu nguồn vốn đầu tư.
-
khoa học chậm đổi mới.
-
thiếu nguyên, nhiên liệu.
-
thị trường bị thu hẹp.
-
thiếu nguồn vốn đầu tư.
-
khoa học chậm đổi mới.
Vấn đề dân cư mà Nhà nước Liên bang Nga quan tâm nhất hiện nay là
-
dân số giảm và già hóa dân số.
-
nhiều dân tộc.
-
mật độ dân số thấp.
-
đô thị hóa tự phát.
-
dân số giảm và già hóa dân số.
-
nhiều dân tộc.
-
mật độ dân số thấp.
-
đô thị hóa tự phát.
Ở Việt Nam, vùng sẽ chịu ảnh hưởng nặng nề nhất của biến đổi khí hậu do nước biển dâng là
-
Đồng bằng sông Cửu Long.
-
Trung du và miền núi Bắc Bộ.
-
Đồng bằng sông Hồng.
-
Duyên hải Nam Trung Bộ
-
Đồng bằng sông Cửu Long.
-
Trung du và miền núi Bắc Bộ.
-
Đồng bằng sông Hồng.
-
Duyên hải Nam Trung Bộ
Phát biểu nào sau đây không đúng với khí hậu phần lãnh thổ phía Bắc nước ta (từ dãy Bạch Mã trở ra)?
-
Biên độ nhiệt độ trung bình năm nhỏ.
-
Trong năm có một mùa đông lạnh.
-
Có 2 – 3 tháng nhiệt độ dưới 180C.
-
Nhiệt độ trung bình năm trên 200C.
-
Biên độ nhiệt độ trung bình năm nhỏ.
-
Trong năm có một mùa đông lạnh.
-
Có 2 – 3 tháng nhiệt độ dưới 180C.
-
Nhiệt độ trung bình năm trên 200C.
Căn cứ và Atlat Địa lí Việt Nam trang 14, cho biết sông Đồng Nai bắt nguồn từ cao nguyên nào sau đây?
-
Mơ Nông.
-
Lâm Viên.
-
Di Linh.
-
ĐắkLắk.
-
Mơ Nông.
-
Lâm Viên.
-
Di Linh.
-
ĐắkLắk.
Cho bảng số liệu:

Theo bảng số liệu, để thể hiện tốc độ tăng trưởng lao động phân theo khu vực kinh tế nước ta giai đoạn 2009 – 2019, dạng biểu đồ nào sau đây là thích hợp nhất?
-
Đường
-
Tròn
-
Miền.
-
Cột.
-
Đường
-
Tròn
-
Miền.
-
Cột.
Ý nào dưới đây không đúng với sự chuyển dịch cơ cấu ngành công nghiệp nước ta hiện nay?
-
Giảm tỉ trọng công nghiệp chế biến.
-
Giảm tỉ trọng công nghiệp sản xuất, phân phối điện, khí đốt, nước.
-
Tăng tỉ trọng công nghiệp chế biến.
-
Giảm tỉ trọng công nghiệp khai thác.
-
Giảm tỉ trọng công nghiệp chế biến.
-
Giảm tỉ trọng công nghiệp sản xuất, phân phối điện, khí đốt, nước.
-
Tăng tỉ trọng công nghiệp chế biến.
-
Giảm tỉ trọng công nghiệp khai thác.
Ở nước ta, trong các ngành giao thông vận tải sau, ngành nào có ý nghĩa quan trọng đối với vận tải quốc tế?
-
Đường biển, đường hàng không.
-
Đường bộ, đường hàng không.
-
Đường biển, đường sông.
-
Đường sắt, đường biển.
-
Đường biển, đường hàng không.
-
Đường bộ, đường hàng không.
-
Đường biển, đường sông.
-
Đường sắt, đường biển.
Tây Nguyên hiện nay phát triển mạnh
-
thủy điện, cây công nghiệp nhiệt đới
-
sản xuất lúa gạo, nuôi trồng thủy sản
-
khai thác gỗ tròn, trồng cây dược liệu
-
khai thác các khoáng sản, sản xuất ô tô
-
thủy điện, cây công nghiệp nhiệt đới
-
sản xuất lúa gạo, nuôi trồng thủy sản
-
khai thác gỗ tròn, trồng cây dược liệu
-
khai thác các khoáng sản, sản xuất ô tô
Vấn đề quan trọng trong phát triển nông nghiệp theo chiều sâu ở Đông Nam Bộ là
-
thủy lợi, thay đổi cơ cấu cây trồng.
-
cải tạo đất, thay đổi cơ cấu cây trồng.
-
thay đổi cơ cấu cây trồng, chống xói mòn.
-
áp dụng kĩ thuật canh tác tiên tiến, thủy lợi.
-
thủy lợi, thay đổi cơ cấu cây trồng.
-
cải tạo đất, thay đổi cơ cấu cây trồng.
-
thay đổi cơ cấu cây trồng, chống xói mòn.
-
áp dụng kĩ thuật canh tác tiên tiến, thủy lợi.
Hai hạt nhân ${ }_3^1 \mathrm{H}$ và ${ }_2^3 \mathrm{He}$ có cùng
-
số nuclôn.
-
số nơtron.
-
điện tích.
-
số prôtôn.
-
số nuclôn.
-
số nơtron.
-
điện tích.
-
số prôtôn.
Cho đòng điện có cường độ 2(A) chạy qua bình điện phân đựng dung địch muối đồng có cực dương bằng đồng trong 11 giở 44 phút 2020 giây. Khối lượng đồng bám vào cực âm là
-
$2,56 \mathrm{~g}$
-
$2,65 \mathrm{~g}$
-
$5,62 \mathrm{~g}$
-
$6,25 \mathrm{~g}$
-
$2,56 \mathrm{~g}$
-
$2,65 \mathrm{~g}$
-
$5,62 \mathrm{~g}$
-
$6,25 \mathrm{~g}$
Hai quả cầu nhỏ giống nhau đặt trong không khi. Một quả mang điện tích $1,92 \mathrm{pC}$ và một quả không mang điện. Cho hai quả cầu tiếp xúc đến khi cân bằng điện rồi tách chúng ra cách nhau $3 \mathrm{~cm}$ . Số electron mà hai quả trao đổi là:
-
$6 \cdot 10^6$
-
$6 \cdot 10^5$
-
$6.10^4$ .
-
$6.10^7$ .
-
$6 \cdot 10^6$
-
$6 \cdot 10^5$
-
$6.10^4$ .
-
$6.10^7$ .
Trong thí nghiệm khe Young ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm $\mathrm{A}, \mathrm{B}$ đối xứng qua vân trung tâm, khi màn cách hai khe một khoảng là $\mathrm{D}$ thì $\mathrm{A}, \mathrm{B}$ là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng dd thỉ $A, B$ là vân sáng và đếm được số vân sáng trên đoạn $A B$ trước và sau khi dịch chuyển màn hơn kém nhau 4. Nếu dịch tiếp màn ra xa hai khe một khoàng $9 \mathrm{~d}$ nữa thì $\mathrm{A}, \mathrm{B}$ lại là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại $\mathrm{A}$ và $\mathrm{B}$ không còn xuất hiện vân sáng nữa. Tại $\mathrm{A}$ khi chưa dịch chuyền màn là vân sáng thử mấy?
-
6
-
5
-
4
-
7
-
6
-
5
-
4
-
7
Một sóng điện từ có tần số $2 \cdot 10^7 \mathrm{~Hz}$ đang lan truyền trong chân không. Lấy $\mathrm{c}=3 \cdot 10^8 \mathrm{~m} / \mathrm{s}$ . Bước sóng của sóng điện từ này là
-
$15 \mathrm{~m}$
-
$0,07 \mathrm{~m}$
-
$150 \mathrm{~m}$
-
$0,7 \mathrm{~m}$
-
$15 \mathrm{~m}$
-
$0,07 \mathrm{~m}$
-
$150 \mathrm{~m}$
-
$0,7 \mathrm{~m}$
Đặt điện áp xoay chiều $u=U_0 \cos (100 \pi t)$ vào hai đầu tụ điện có điện dung $\quad C=\frac{50}{\pi}(\mu \mathrm{F})$
Dung kháng của tụ điện là
-
$200 \Omega$ .
-
$50 \Omega$ .
-
$100 \Omega$ .
-
$400 \Omega$ .
-
$200 \Omega$ .
-
$50 \Omega$ .
-
$100 \Omega$ .
-
$400 \Omega$ .
Đồ thị dưới đây biểu điễn động năng cực đại $\mathrm{E}$ của êlectron thoát ra khỏi bề mặt của một tẩm kali thay đổi theo tần số $\mathrm{f}$ của bức xạ điện từ tới tấm. Từ đồ thịa giá trị của hằng số Plăng có giá trị gần nhất với giá trị nào sau đây?
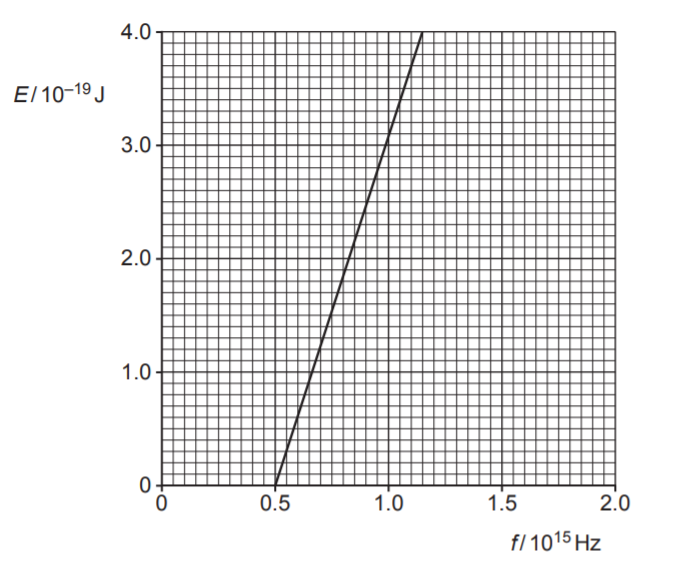
-
$6,2 \cdot 10^{-34} \mathrm{~J}$ .s.
-
$6,6 \cdot 10^{-34} \mathrm{~J}$ .s.
-
$6,2 \cdot 10^4 \mathrm{~J}$ .s.
-
$1,6.10^{33} \mathrm{~J} . \mathrm{s}$ .
-
$6,2 \cdot 10^{-34} \mathrm{~J}$ .s.
-
$6,6 \cdot 10^{-34} \mathrm{~J}$ .s.
-
$6,2 \cdot 10^4 \mathrm{~J}$ .s.
-
$1,6.10^{33} \mathrm{~J} . \mathrm{s}$ .
Một con cá heo nghe được âm thanh trong tần số $150 \mathrm{~Hz}-150 \mathrm{kHz}$ . Cả người và cá heo có thể nghe được âm thanh có tần số nào đưới đây?
-
$150 \mathrm{~Hz}-20 \mathrm{kHz}$ .
-
$20 \mathrm{~Hz}-150 \mathrm{~Hz}$ .
-
$20 \mathrm{~Hz}-150 \mathrm{kHz}$ .
-
$20 \mathrm{kHz}-150 \mathrm{kHz}$ .
-
$150 \mathrm{~Hz}-20 \mathrm{kHz}$ .
-
$20 \mathrm{~Hz}-150 \mathrm{~Hz}$ .
-
$20 \mathrm{~Hz}-150 \mathrm{kHz}$ .
-
$20 \mathrm{kHz}-150 \mathrm{kHz}$ .
Hai con lắc đơn giống hệt nhau mà các vật nhỏ mang điện tích như nhau, được treo ở một nơi trên mặt đất. Trong mỗi vùng không gian chứa mỗi con lắc có một điện trường đều. Hai điện trường này có cùng cường độ nhưng các đường sức hợp với nhau một góc $\alpha$ . Giữ hai con lắc ở vị trí các dây treo có phương thẳng đứng rồi thả nhẹ thì chúng dao động điều hòa trong củng một mặt phẳng với biên độ góc $8^{\circ}$ và có chu kì tương ửng là $T_1$ và $T_2$ . Nếu $T_2>T_1$ thì $\alpha$ không thể nhận giá trị nào sau đây?
-
$170^{\circ}$
-
$30^{\circ}$
-
$90^{\circ}$
-
$160^{\circ}$
-
$170^{\circ}$
-
$30^{\circ}$
-
$90^{\circ}$
-
$160^{\circ}$
Một khối thưy tinh được giữ trên bề mặt một chất lỏng chiết suất n. Tia sáng từ không khí tới bề mặt thủy tinh với góc tới $42^{\circ}$, góc khúc xạ trong thủy tinh là $27^{\circ}$ thì bắt đầu xày ra hiện tượng phàn xạ toàn phần tại bề mặt tiếp xúc giữa thủy tinh và chất lòng (hình vê). Tính chiết suất của chất löng.
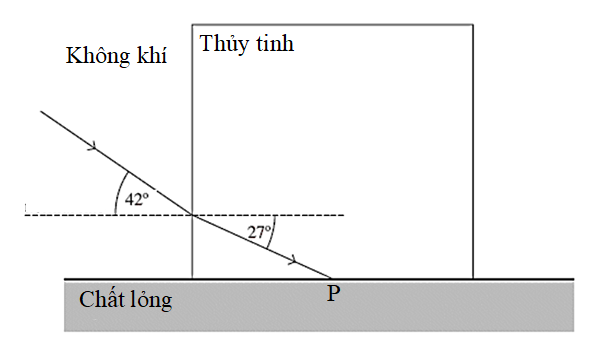
-
1,3
-
0,4
-
2.3
-
3.1
-
1,3
-
0,4
-
2.3
-
3.1
Đốt cháy hoàn toàn 0,1 mol hỗn hợp gồm X gồm C6H14 và CxHx (CxHx có vòng benzen) thu được 15,68 lít khí CO2 (đktc) và 9,9 gam nước. Nếu cho hỗn hợp trên vào dung dịch Br2 dư thì CxHx tác dụng hoàn toàn với m gam Br2 . Giá trị của m là
-
8.
-
32.
-
16.
-
4.
-
8.
-
32.
-
16.
-
4.
Cho 0,25 molMgO tan hoàn toàn trong một lượng vừa đủ dung dịch H2SO4 25% đun nóng, sau đó làm nguội dung dịch đến 10oC. Tính khối lượng tinh thể MgSO4.7H2O đã tách ra khỏi dung dịch, biết rằng độ tan của MgSO4 ở 100C là 28,2 gam.
-
23,31 gam.
-
26,61 gam.
-
28,62 gam.
-
19,33 gam.
-
23,31 gam.
-
26,61 gam.
-
28,62 gam.
-
19,33 gam.
Hoà tan 25 gam hỗn hợp $\mathrm{X}$ gồm $\mathrm{FeSO}_4$ và $\mathrm{Fe}_2\left(\mathrm{SO}_4\right)_3$ vào nước, thu được $150 \mathrm{ml}$ dung dịch $\mathrm{Y}$ . Thêm $\mathrm{H}_2 \mathrm{SO}_4$ (dư) vào $20 \mathrm{ml}$ dung dịch $\mathrm{Y}$ rồi chuẩn độ toàn bộ dung dịch này bằng dung dịch $\mathrm{KMnO}_4 0,1 \mathrm{M}$ thì dùng hết $30 \mathrm{ml}$ dung dịch chuẩn. Phần trăm khối lượng $\mathrm{FeSO}_4$ trong hỗn hợp $\mathrm{X}$ là
-
$68,4 \%$ .
-
$9,12 \%$ .
-
$31,6 \%$ .
-
$13,68 \%$ .
-
$68,4 \%$ .
-
$9,12 \%$ .
-
$31,6 \%$ .
-
$13,68 \%$ .
Cho $\mathrm{m}$ gam hỗn hợp $\mathrm{X}$ gồm $\mathrm{H}_2 \mathrm{NCH}_2 \mathrm{CH}_2 \mathrm{COOH}$ và $\mathrm{CH}_3 \mathrm{CH}\left(\mathrm{NH}_2\right) \mathrm{COOH}$ tác dụng với $200 \mathrm{ml}$ dung dịch $\mathrm{NaOH} 1 \mathrm{M}$ thu được dung dịch $\mathrm{Y}$ . Biết dung dịch $\mathrm{Y}$ tác dụng vừa đủ với $500 \mathrm{ml}$ dung dịch $\mathrm{HCl} 1 \mathrm{M}$ . Giá trị của m là
-
26,7 .
-
17,8 .
-
13,35 .
-
22,25 .
-
26,7 .
-
17,8 .
-
13,35 .
-
22,25 .
Thực hiện thí nghiệm như hình vẽ bên. Khi đun nóng bình cầu ở nhiệt độ ≥ 170oC thì hiện tượng xảy ra trong ống nghiệm đựng dung dịch brom là
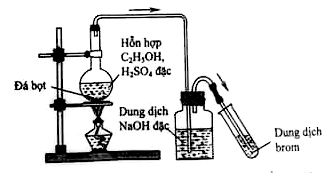
-
dung dịch brom bị nhạt màu.
-
có kết tủa màu trắng xuất hiện.
-
có kết tủa màu vàng nhạt xuất hiện.
-
có kết tủa màu xanh xuất hiện.
-
dung dịch brom bị nhạt màu.
-
có kết tủa màu trắng xuất hiện.
-
có kết tủa màu vàng nhạt xuất hiện.
-
có kết tủa màu xanh xuất hiện.
Phát biểu nào sau đây đúng?
-
Tơ tằm thuộc loại tơ thiên nhiên.
-
Amilozơ có cấu trúc mạch phân nhánh.
-
Tinh bột là một loại polime bán tổng hợp.
-
Tơ visco thuộc loại tơ tổng hợp.
-
Tơ tằm thuộc loại tơ thiên nhiên.
-
Amilozơ có cấu trúc mạch phân nhánh.
-
Tinh bột là một loại polime bán tổng hợp.
-
Tơ visco thuộc loại tơ tổng hợp.
Nhiệt phân hoàn toàn muối nitrat của kim loại hóa trị II không đổi thu được 6 gam oxit và 8,4 lít (đktc) hỗn hợp khí NO2, O2. Công thức hóa học của muối là
-
Mg(NO3)2.
-
Cu(NO3)2.
-
Pb(NO3)2.
-
Zn(NO3)2.
-
Mg(NO3)2.
-
Cu(NO3)2.
-
Pb(NO3)2.
-
Zn(NO3)2.
Cho các chất sau tan trong nước: Na2CO3, CH3COOCH3, HCOOH, MgCl2, HF. Số chất điện li mạnh và điện li yếu lần lượt là
-
2 và 2.
-
3 và 2.
-
1 và 4.
-
3 và 1.
-
2 và 2.
-
3 và 2.
-
1 và 4.
-
3 và 1.
Cho 5 gam kẽm viên vào cốc đựng 50 ml dung dịch H2SO4 4M ở nhiệt độ thường (25oC). Trường hợp nào tốc độ phản ứng không đổi?
-
Dùng lượng dung dịch H2SO4 gấp đôi ban đầu.
-
Thay dung dịch H2SO4 4M bằng dung dịch H2SO4 2M.
-
Thay 5 gam kẽm viên bằng 5 gam kẽm bột.
-
Thực hiện phản ứng ở 50oC.
-
Dùng lượng dung dịch H2SO4 gấp đôi ban đầu.
-
Thay dung dịch H2SO4 4M bằng dung dịch H2SO4 2M.
-
Thay 5 gam kẽm viên bằng 5 gam kẽm bột.
-
Thực hiện phản ứng ở 50oC.
Hỗn hợp M gồm 3 este đơn chức X, Y, Z (MX< MY< MZ và số mol của Y bé hơn số mol X) tạo thành từ cùng một axitcacboxylic (phân tử chỉ có nhóm COOH) và ba ancol no (số nguyên tử C trong phân tử mỗi ancol nhỏ hơn 4). Thủy phân hoàn toàn 34,8 gam M bằng 490 ml dung dịch NaOH 1M (dư 40% so với lượng phản ứng). Cô cạn hỗn hợp sau phản ứng thu được 38,5 gam chất rắn khan. Mặt khác, nếu đốt cháy hoàn toàn 34,8 gam M thì thu được CO2 và 23,4 gam H2O. Thành phần phần trăm theo khối lượng Y trong M là
-
32,18%.
-
25,32%
-
44,11%
-
16,95%
-
32,18%.
-
25,32%
-
44,11%
-
16,95%
Cây không sử dụng được nitơ phân tử N2 trong không khí vì:
-
phân tử N2 có liên kết ba bền vững cần phải đủ điều kiện mới bẻ gãy được.
-
lượng N2 tự do bay lơ lửng trong không khí không hòa vào đất
Nên cây không hấp thụ được.
-
lượng N2 trong không khí quá thấp.
-
do lượng N2 có sẵn trong đất từ các nguồn khác quá lớn.
Giải chi tiết:
Cây không sử dụng được nitơ phân tử N2 trong không khí
Vì phân tử N2 có liên kết ba bền vững cần phải đủ điều kiện mới bẻ gãy được.
-
phân tử N2 có liên kết ba bền vững cần phải đủ điều kiện mới bẻ gãy được.
-
lượng N2 tự do bay lơ lửng trong không khí không hòa vào đất
Nên cây không hấp thụ được. -
lượng N2 trong không khí quá thấp.
-
do lượng N2 có sẵn trong đất từ các nguồn khác quá lớn.
Giải chi tiết:
Cây không sử dụng được nitơ phân tử N2 trong không khí
Vì phân tử N2 có liên kết ba bền vững cần phải đủ điều kiện mới bẻ gãy được.
Trạng thái có sự biến đổi lí hoá xảy ra trong tế bào sống khi bị kích thích gọi là
-
trạng thái hưng phấn.
-
trạng thái ức chế
-
trạng thái tiềm sinh
-
trạng thái nghỉ
-
trạng thái hưng phấn.
-
trạng thái ức chế
-
trạng thái tiềm sinh
-
trạng thái nghỉ
Cho các ý sau:
1. Ức chế sinh trưởng của chồi đỉnh.
2. Kích thích sinh trưởng của các chồi bên.
3. Tạo ưu thế đỉnh cho cây..
Khi trồng các loại hoa màu, người ta thường ngắt bỏ ngọn bí, mướp, dưa, …. Việc này có tác dụng:
-
1, 2.
-
2, 3.
-
1, 3.
-
1, 2, 3.
-
1, 2.
-
2, 3.
-
1, 3.
-
1, 2, 3.
Cơ sở tế bào học đặc trưng chỉ có ở sinh sản hữu tính là
-
quá trình giảm phân và thụ tinh.
-
quá trình nguyên phân và giảm phân.
-
kiểu gen của thế hệ sau không thay đổi.
-
bộ nhiễm sắc thể của loài không thay đổi.
-
quá trình giảm phân và thụ tinh.
-
quá trình nguyên phân và giảm phân.
-
kiểu gen của thế hệ sau không thay đổi.
-
bộ nhiễm sắc thể của loài không thay đổi.
Dạng đột biến nào sau đây làm cho alen đột biến tăng 2 liên kết hiđrô?
-
Thêm 1 cặp A – T.
-
Mất 2 cặp A – T.
-
Thêm 1 cặp G – X.
-
Mất 1 cặp A – T.
-
Thêm 1 cặp A – T.
-
Mất 2 cặp A – T.
-
Thêm 1 cặp G – X.
-
Mất 1 cặp A – T.
Một quần thể có thành phần kiểu gen là: 0,04AA : 0,32Aa : 0,64aa. Tần số alen a của quần thể này là bao nhiêu?
-
0,8.
-
0,2.
-
0,5.
-
0,3.
-
0,8.
-
0,2.
-
0,5.
-
0,3.
Theo giả thuyết siêu trội, phép lai nào sau đây cho đời con có ưu thế lai cao nhất?
-
AAbbdd × aaBBDD.
-
AaBbdd × aabbdd.
-
AAbbdd × aabbDD.
-
. AABBDD × AABBDD.
-
AAbbdd × aaBBDD.
-
AaBbdd × aabbdd.
-
AAbbdd × aabbDD.
-
. AABBDD × AABBDD.
Các loài sâu ăn lá thường có màu xanh lẫn với màu xanh của lá, nhờ đó mà chúng khó bị chim ăn sâu phát hiện và tiêu diệt. Theo Đacuyn, đặc điểm thích nghi này được hình thành do
-
chọn lọc tự nhiên tích lũy các biến dị cá thể màu xanh qua nhiều thế hệ.
-
ảnh hưởng trực tiếp của thức ăn là lá cây có màu xanh làm biến đổi màu sắc cơ thể sâu.
-
khi chuyển sang ăn lá, sâu tự biến đổi màu để thích nghi với môi trường.
-
Chim ăn sâu không ăn các con sâu màu xanh
-
chọn lọc tự nhiên tích lũy các biến dị cá thể màu xanh qua nhiều thế hệ.
-
ảnh hưởng trực tiếp của thức ăn là lá cây có màu xanh làm biến đổi màu sắc cơ thể sâu.
-
khi chuyển sang ăn lá, sâu tự biến đổi màu để thích nghi với môi trường.
-
Chim ăn sâu không ăn các con sâu màu xanh
Quần thể sinh vật là
-
tập hợp cá thể cùng loài, cùng sinh sống trong một không gian xác định, vào một thời gian nhất định, có khả năng sinh sản bình thường
-
tập hợp cá thể khác loài, cùng sinh sống trong một không gian xác định, vào một thời gian nhất định, có sự cách ly sinh sản giữa các cá thể.
-
nhóm cá thể cùng loài, tồn tại trong một thời gian nhất định, cùng sinh sống trong vùng phân bố của loài.
-
nhóm cá thể của một loài, tồn tại trong một thời gian nhất định, có khả năng sinh sản thế hệ mới hữu thụ
-
tập hợp cá thể cùng loài, cùng sinh sống trong một không gian xác định, vào một thời gian nhất định, có khả năng sinh sản bình thường
-
tập hợp cá thể khác loài, cùng sinh sống trong một không gian xác định, vào một thời gian nhất định, có sự cách ly sinh sản giữa các cá thể.
-
nhóm cá thể cùng loài, tồn tại trong một thời gian nhất định, cùng sinh sống trong vùng phân bố của loài.
-
nhóm cá thể của một loài, tồn tại trong một thời gian nhất định, có khả năng sinh sản thế hệ mới hữu thụ
Bệnh bạch tạng ở người do đột biến gen lặn a nằm trên nhiễm sắc thể thường quy định, alen trội A tương ứng quy định người bình thường. Một gia đình có bố và mẹ bình thường nhưng người con đầu của họ bị bạch tạng. Khả năng để họ sinh đứa con thứ hai cũng bị bệnh bạch tạng là bao nhiêu?
-
¼
-
½
-
1/3
-
¾
-
¼
-
½
-
1/3
-
¾




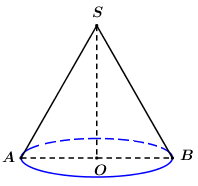
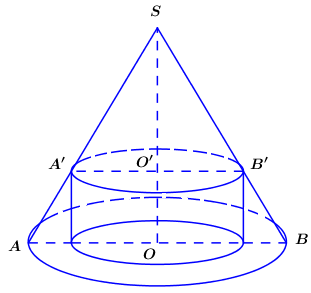
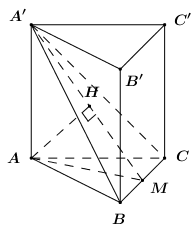



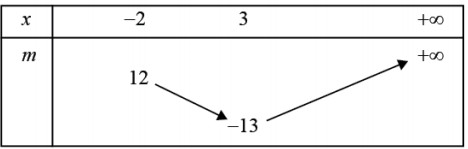

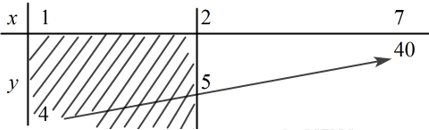
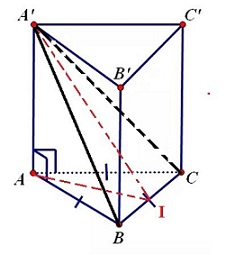
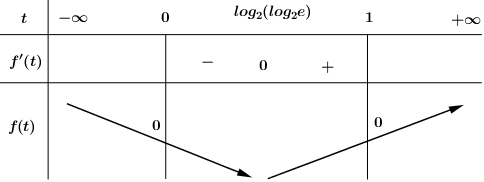
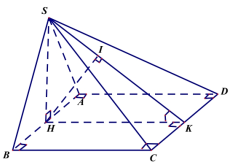

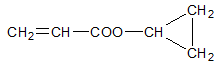 (c mol)
(c mol)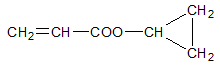 (b mol)
(b mol)